Giới thiệu về bài toán

Ta sử dụng bài toán ex4 trong khóa học Machine Learning của Andrew Ng.

Bài toán đưọc mô tả như sau:
Cho tập dữ liệu ex4Data.zip chứa dữ liệu của 40 sinh viên đậu và 40 sinh viên rớt đại học. Mỗi mẫu \((x^{(i)}, y^{(i)})\) chứa điểm số của 2 bài kiểm tra và kết quả thi của một sinh 1 viên.
Nhiệm vụ của ta là xây dựng một mô hình phân loại để ước lượng cơ hội đậu hay rớt của một sinh viên thông qua điểm của 2 bài kiểm tra.

Trong tập dữ liệu huấn luyện, ta có:

a. Cột đầu tiên của dữ liệu X đại diện cho điểm bài thi thứ 1 và cột thứ 2 đại diện cho điểm bài thi thứ 2.
b. Vector Y sử dụng ‘1’ là lable cho sinh viên đậu và ‘0’ là lable cho sinh viên rớt.

Biểu diễn dữ liệu

Tập dữ liệu được biểu diễn như sau

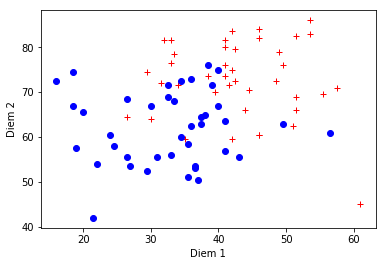
Với điểm màu đỏ biểu diễn cho sinh viên là đậu và màu xanh là rớt.

Tìm lời giải.

Hàm Logistic

\[ \sigma{(t)} = \frac{1}{1+e^{-t}} \]

Hàm này có đồ thị như sau:

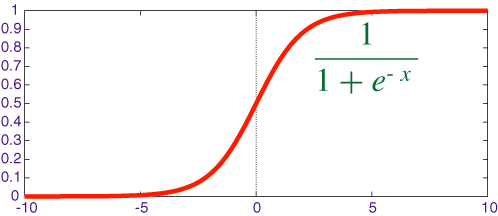
• Có miền xác định \( \mathbb{R} \) và giá trị từ 0 đến 1.
• Tồn đại đạo hàm tại mọi điểm.
• Phù hợp cho việc phân loại (có là 1, không là 0)

Tìm hàm mất mát ( loss function )

Ta gọi
\( D = {(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),…,(x^{(n)},y^{(n)})}, \forall x^{(i)} \in \mathbb{R}^d , y^{(i)} \in \{0,1\} \)
là tập dữ liệu đề cho với n là số lượng điểm dữ liệu.
Mục tiêu của ta là cho dữ liệu của một sinh viên bất kỳ, dự đoán sinh viên đó đậu hay rớt.
\[ x^{(i)} \Rightarrow \hat{h}^{(i)} \] Đặt \( Y^{(i)} \) là giá trị của \( y^{(i)} \) với đầu vào là \( x^{(i)} \). Ta có \( Y^{(i)} \) tuân theo phân phối Bernouli. \[ Y^{(i)} \sim Bernouli(p,n) \] Với: \[ p = P{(y=1|x,w)} = \sigma {(w^Tx)} \] với \( w = [w_0, w_1, …, w_d]^T \) là tham số cần ước lượng và \( x^{(i)} = [1, x ^{(i)} _ {1}, …, x ^{(i)} _ {d} ]^T \)
Để thuận tiện trong việc viết, ta đặt \( \alpha^{(i)} = \sigma (w^Tx^{(i)}) \) \[ q = P{(y=0|x^{(i)},w)} = 1 - p = 1 - \alpha^{(i)} \] Từ đó ta suy ra: \[ P{(y^{(i)}|x^{(i)},w)} = (\alpha^{(i)})^{y^{(i)}}(1-\alpha^{(i)})^{1-y^{(i)}} \] Tức là khi \( y^{(i)} = 1 \) vế phải còn lại \( \alpha^{(i)} \) và khi \( y^{(i)} = 0 \) vế phải còn lại \( 1 - \alpha^{(i)} \). Ta muốn mô hình này tốt nhât (Sát giá trị với thực tế nhất) tức là xác suất này phải lớn nhất.
Xét trên toàn bộ tập dữ liệu D. Ta có thể viết lại likelihood của parameters là: \[ \begin{eqnarray} L(W) &=& P( \vec{y} | X,W ) \
&=& \prod_{i=1}^{n} P{(y^{(i)}|x^{(i)},w)} \
&=& \prod_{i=1}^{n}(\alpha^{(i)})^{y^{(i)}}(1-\alpha^{(i)})^{1-y^{(i)}}
\end{eqnarray} \] Mục tiêu của ta là maximize giá trị \( L(w) \) trên.

negative log likelihood.

Với hàm số trên, việc tối ưu là rất khó vì khi số \(n\) lớn thì giá trị của \(P{(y^{(i)}|x^{(i)},w)}\) sẽ rât nhỏ. Ta sẽ lầy logarit cơ số e của \( L(w) \). Sau đó lấy ngược dấu để được một hàm số mới có giá trị lớn hơn và là một hàm lồi (convex function). Lúc này bài toán ta trở thành tìm giá trị nhỏ nhất của hàm mất mát (hàm này thường được gọi là negative log likelihood ). \[ J{(w)} = -log( L(w) ) = -\sum_{i=1}^{n}(y^{(i)} log(\alpha^{(i)}) + (1-y^{(i)})log(1-\alpha^{(i)})) \] Vì \( L(w) \in (0,1) \Rightarrow -log(P{(Y|w)}) > 0 \)
Lúc này ta được \( J{(w)} \) làm một hàm lồi nên ta có thể áp dụng các bài phương pháp tối ưu lồi (convex optimization ) để giải quyết bài toán này.

Gradient Descent method

Gradient Descent là một phương pháp tối ưu sử dụng phổ biến trong bài toán tối ưu lồi. Xét khảo sát một hàm số như hình vẽ

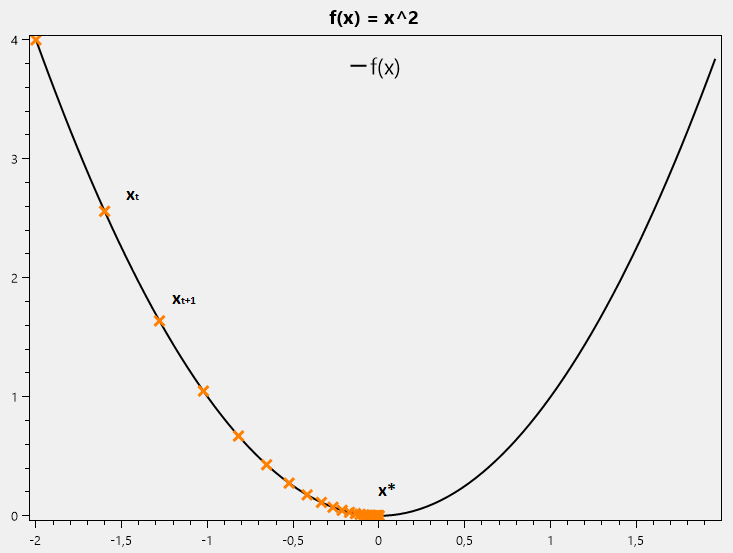gọi \( x* \) là điểm cực trị cần tìm của hàm \(f_{(x)}\)
Nếu đạo hàm của hàm số tại \(x_t: f’_ {x_t} > 0 \) thì \(x_t\) nằm về phía phải so với \(x*\).
Vậy muốn đến được \(x*\) ta cần di chuyển \(x_t\) về phía trái.

Và ngược lại, nếu đạo hàm của hàm số tại \(x_t: f’_ {x_t} < 0 \) thì \(x_t\) nằm về phía trái so với \(x*\).
Vậy muốn đến được \(x*\) ta cần di chuyển \(x_t\) về phía phải.

Một cách tổng quát, ta cần cộng cho \(x_t\) một lượng \( \Delta \)ngược dấu với đạo hàm: \[ x_{t+1} = x_t + \Delta \]

Nếu \(x_t\) càng xa \(x*\) thì \( f’_ {x_t} \) càng lớn nên lượng \( \Delta \) sẽ tỉ lệ với đạo hàm.
Từ đó ta suy ra được: \[ x_{t+1} = x_t - \alpha f’_ {x_t} \] Với \( \alpha > 0 \) gọi là learning rate.

Tổng quát với hàm nhiều biến ta có: Với hàm \( h{(X)} = w_0 + x_1w_1 + … + x_nw_n \): \[ X_{t+1} = X_t -\alpha \nabla_X f_{(X_t)} \]

với \( \nabla_X f_{(X_t)} \) là gradient của \(f\) theo biến \(X\)

Ví dụ:
Cho hàm số \[f{(x)} = x^2 \] Với điểm ban đầu \(x_0 = 2\) và \(\alpha = 0.6 \) ta được: \[ f’ _ {x} = 2x \] \[ x_{1} = x_0 - \alpha f’_ {x_0} = x_0 - 0.6\times 2x_0 = -0.2x_0\] \[ \Rightarrow x_t = (-0.2)^t \times x_0 \] Với t càng lớn thì giá trị \(x_t\) càng gần 0 nên kết quả của ta càng chính xác.
Tuy nhiên nếu ta chọn \(x_0 = 2\) và \(\alpha = 0.5 \) thì: \[ x_{1} = x_0 - \alpha f’_ {x_0} = x_0 - 0.5\times 2x_0 = 0\] Vậy là ta đã tìm được giá trị cực trị của \(f{(x)}\) ngay tại lần lặp đầu tiên. Từ đó ta thấy việc chọn \(\alpha\) và \(x_0\) khác nhau sẽ ảnh hưởng đến kết quả và số lần lặp của thuật toán.

Newton’s method

Để tìm cực trị của hàm \( g{(x)} \), ta cần tìm nghiệm của phương trình \( g’_ {x} = 0\).

Xuất phát từ định lý taylor:
\[ f{(x)} = f{(x_0)} + f’ {(x_0)}.(x-x_0) \]
Tìm x để \[ f{(x)} = 0 \] \[ \Leftrightarrow f{(x_0)} + f’ {(x_0)}.(x-x_0) = 0 \] \[ \Rightarrow x = x_0 - \frac{f{(x_0)}}{f’ {(x_0)}} \] Đặt \( f = g’ \) thì nghiệm của phương trình \( g’ {x} = 0\) là: \[ x_{t+1} = x_t - \frac{g’ {(x_0)}}{g’’ {(x_0)}}\] Tổng quá hóa cho hàm nhiều biến: \[ X_{t+1} = X_t - \mathbb{H}^{-1} \nabla _ {x} f{(X_t)}\] Với \( H \) là ma trận Hessian.

Ví dụ:
Cho hàm số \[ f{(x)} = x^2 -2x + 1 \] với điểm ban đầu là \(x_0 = 3\) ta được: \[ f’ {(x)} = 2x - 2 \] \[ f’’ {(x)} = 2 \] \[ x_1 = x_0 - \frac{f’}{f’’} = x_0 - \frac{2x_0-2}{2} = 1 \] Vậy với hàm bậc 2 một biến thì chỉ sau 1 lần lặp ta đã tìm được giá trị cực trị.

Giải bài toán

Trở lại với bài toán ban đầu, ta đã có được 2 phương pháp tối ưu hàm mất mát \( J \). Ta sẽ giải bài này dùng phương pháp tối ưu Newton’s method.
Ta có hàm mất mát: \[ J{(w)} = -\sum_{i=1}^{n}(y^{(i)} log(\alpha^{(i)}) + (1-y^{(i)})log(1-\alpha^{(i)})) \]

Áp dụng công thức Newton:

\[ w_{t+1} = w_t - \mathbb{H}^{-1} \nabla _ {w} J{(w_t)}\] Ta cần phải tính đạo hàm bậc nhất và bậc 2 của hàm mất mát trước. \[ log \alpha ^{(i)} = log \frac{1}{1+e^{-w^Tx^{(i)}}} = -log(1+e^{-w^Tx^{(i)}}) \] \[ \frac{\partial log \alpha ^{(i)}}{\partial w_j} = \frac{x _ {j} ^ {(i)} e^{-w^Tx^{(i)}}}{1+e^{-w^Tx^{(i)}}} = x _ {j} ^{(i)} (1 - \alpha ^{(i)} ) \] \[ log(1-\alpha ^{(i)}) = log \frac{e^{-w^Tx^{(i)}}}{1+e^{-w^Tx^{(i)}}} = -w^Tx^{(i)} - log(1+e^{-w^Tx^{(i)}}) \] \[ \frac{\partial log(1-\alpha ^{(i)}) }{\partial w_j} = - x _ {j} ^ {(i)} + x _ {j} ^ {(i)} (1-\alpha^{(i)}) = -\alpha^{(i)}x _ {j} ^ {(i)} \] Ta thay vào để tính đạo hàm \( J{(w)} \) ta được:

\[ \begin{eqnarray} \frac{ \partial J{(w)} }{ \partial w_j } &=& - \sum_{j=1}^{n}( y^{(i)} x _ {j} ^ {(i)} (1 - \alpha ^ {(i)} ) - ( 1 - y^{(i)} ) x _ {j} ^ {(i)} \alpha ^ {(i)} ) ~~&(1)& \
&=& - \sum _ {j=1} ^ {n} ( y^{(i)} x _ {j} ^ {(i)} - y^{(i)} x _ {j} ^{(i)} \alpha ^{(i)} - x _ {j} ^ {(i)} \alpha ^{(i)} + y^{(i)} x _ {j} ^ {(i)} \alpha ^{(i)} ) ~~ &(2)& \
&=& - \sum _ {j=1} ^ {n}( y^{(i)} x _ {j} ^{(i)} - x _ {j} ^{(i)} \alpha ^{(i)} ) ~~ &(3)& \
&=& \sum_{j=1}^{n} x _ {j} ^{(i)}( \alpha^{(i)} - y^{(i)} ) ~~ &(4)& \end{eqnarray} \]

Một cách tổng quát cho hàm nhiều biến: \[ \nabla _ x J = A^T ( \alpha - Y ) \] Với : \[ A = \left[ \begin{matrix} x_{1 1} & x_{1 2} & \dots & x_{1 d} \
x_{2 1} & x_{2 2} & \dots & x_{2 d} \
\vdots & \vdots & \ddots & \vdots \
x_{n 1} & x_{n 2} & \dots & x_{n d} \end{matrix} \right] \]

Tính đạo hàm bậc 2 (Hessian):

\[ \partial log \alpha = \frac{\partial \alpha}{\alpha} \] \[ \Rightarrow \partial \alpha = \alpha \partial log \alpha \] \[ \Rightarrow \partial \alpha = \alpha x _ {j} (1 - \alpha ) \] Ta thế vào công thức đạo hàm bậc 2 được.

\[ \begin{eqnarray} \frac{\partial ^ 2 J(w)}{\partial w_j \partial w_k} &=& \sum _{i=1} ^{n} x ^{(i)} _j \left( \frac{\partial \alpha ^{(i)}}{\partial w_k} \right) \
&=& \sum _ {i=1} ^ {n} x^{(i)} _{j} x ^{(i)} _{k} \alpha ^{(i)} (1 - \alpha ^{(i)}) \
&=& {Z} ^{T} _{j} {B} {Z} _{k}
\end{eqnarray} \] với:

\[ {Z}_j = (x ^{(1)} _ j , …, x^{(n)} _j)^T \] \[ {Z}_k = (x ^{(1)} _ k , …, x^{(n)} _k)^T \] \[ {B} = \left[
\begin{matrix} \alpha ^{(1)} (1- \alpha ^{(1)}) & & 0 \
& \ddots & \
0 & & \alpha ^{(1)} (1- \alpha ^{(1)}) \end{matrix} \right] \]

Tổng quát cho hàm nhiều biến, ta được: \[ {H}_w = \nabla ^ 2 _ w J(w) = {A}^T {B} {A} \]

Hiện thực code:
Ở đây ta hiện thực trên ngôn ngữ julia. Ngoài ra ta cũng có thể hiện thực trên matlab/octave, python,.. một cách tương tự.
Ta chia ngẫu nhiên data thành 2 cặp file.

• trx.dat và try.dat chứa điểm của 40 sinh viên và nhãn(đậu/rớt) của sinh viên đó dùng để huấn luyện (train) mô hình.
• tex.dat và tey.dat chứa điểm của 40 sinh viên và nhãn(đậu/rớt) của sinh viên đó dùng để kiểm tra (test) mô hình.

using PyPlot
x = readdlm("trx.dat");
y = readdlm("try.dat");
(m,n) = size(x);
x = reshape(x, m, n);
x = [ones(m,1) x];

theta = zeros(n+1,1);
function g(n)
    return 1.0 ./(1.0+ exp(-n))
end

Iter = 10;
J = zeros(Iter, 1);

# Loop
for i in 1:Iter
    # Calculate the hypothesis fucntion
    z = x*theta;
    # Calculate sigmoid
    h = g(z);
    # Calculate gradient and hession.
    grad = (1/m) .* x' * (h-y);
    H = (1/m) .* x' * diagm(vec(h)) * diagm(vec(1-h)) * x;
    # Calculate J for testing convergence
    J[i] = (1/m)*sum(-y .* log(h) - (1-y) .* log(1-h));
    theta = theta - H\grad;
end
print(theta)

print(J)
print(size(theta))
print( size(x))


tex = readdlm("tex.dat");
tey = readdlm("tey.dat");
#print(size(x));
#print(size(y));
#
(m,n) = size(tex);
tex = reshape(tex, m, n);
# add x_0 (bias)
tex = [ones(m,1) tex];
println(size(tex));

smx = -10:10
smy = g(smx)
plot(smx,smy)

#plot(smx,smy)

resx =  tex * theta;
resy = g(resx);

println(size(resx),size(resy))

plot(resx[1:20],resy[1:20],"r*")
plot(resx[21:40],resy[21:40],"bo")

clx = -10:10
cly = 0.5+0.0 *clx
plot(clx,cly)

succ = 0.
fail = 0.
all = 0.
for i in 1:20
    if resx[i] >= 0.5
        succ +=1
    end
end
println(100. *succ/20)
for i in 21:40
    if resx[i] <0.5
        fail +=1
    end
end
println(100. *fail/20)
println(100 *(succ + fail)/40)

# loss graph
n_loss = 1:Iter
plot( n_loss, J)
xlabel("epoch")
ylabel("loss")

Kết quả thu được như sau:

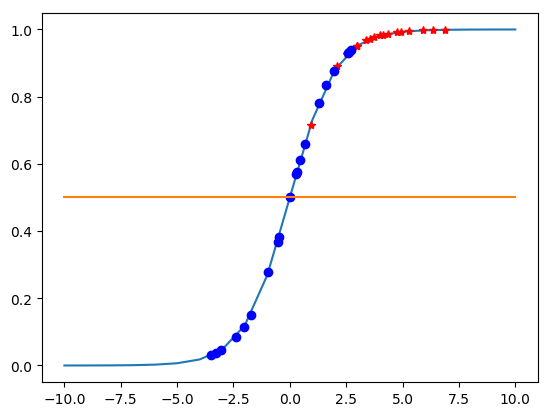
Với đường màu xanh là đồ thị hàm sigmoid, chấm màu xanh là rớt, chấm đỏ là đậu.
Đồ thị của hàm mất mát J(w) như sau:

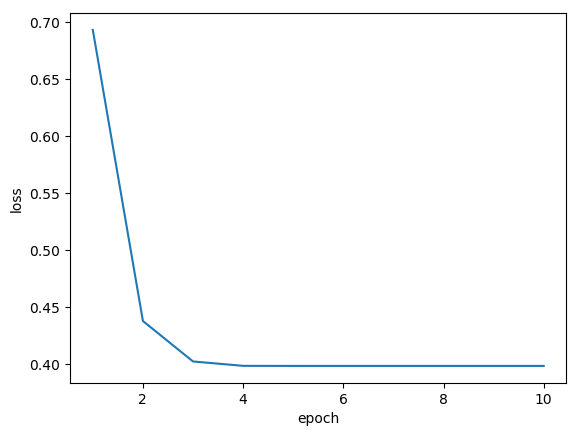
Nếu lấy sinh viên có giá trị y >= 0.5 là đậu và < 0.5 là rớt thì kết quả là dự đoán là:
Sinh viên đậu: 100.0 %
Sinh viên rớt: 65.0 %
Trung bình: 82.5 %

Với tập dữ liệu để huấn luyện (training set) là khá nhỏ (40 sinh viên) thì 82.5% là kết quả chấm nhận được.

Áp dụng phương pháp Gradient Descent:

Đơn giản hơn phương pháp Newton, ở đây ta chỉ tính đạo hàm cấp 1 của hàm mất mát \( J(w) \) và thực hiện lặp.
Ngoài ra ta cần định nghĩa 1 giá trị alpha là Learning rate của thuật toán.
Ở đây ta chọn số lần lặp (iteration) là 500000 và learning rate là 0.005
Hiện thực code quá trình lặp như sau :

# Set iterations
Iter = 500000;
alpha = 0.005;
J = zeros(Iter, 1);
# Loop
for i in 1:Iter
    # Calculate the hypothesis fucntion
    z = x*theta;
    # Calculate sigmoid
    h = g(z);
    # Calculate gradient.
    grad = (1/m) .* x' * (h-y); #' comment
    # Calculate J for testing convergence
    J[i] = (1/m)*sum(-y .* log(h) - (1-y) .* log(1-h));
    theta = theta - alpha*grad;
end
print(theta)

Kết quả thu được như sau:

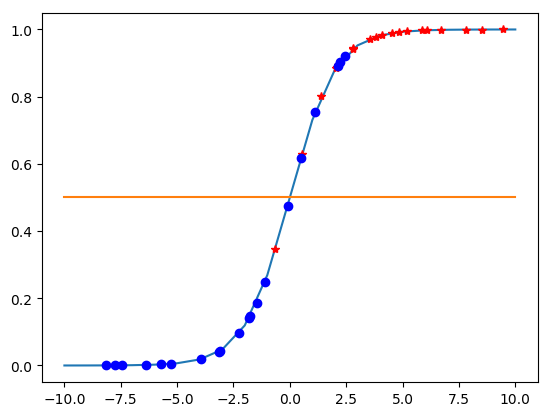
Đồ thị hàm mất mát:

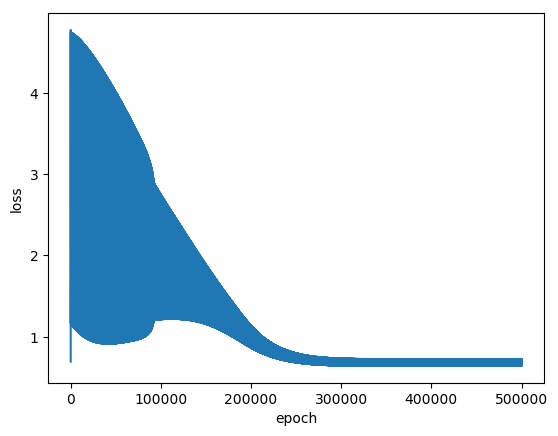
Nếu lấy sinh viên có giá trị y >= 0.5 là đậu và < 0.5 là rớt thì kết quả là dự đoán là:
Sinh viên đậu: 95.0 %
Sinh viên rớt: 80.0 %
Trung bình: 87.5 %

Kết quả ở đây tốt hơn sô với Newton’s method một chút.

Ta thấy được cả Gradient Descent và Newton’s method đều có thể dùng để tối ưu hóa bài toán trên. Tuy kết quả Gradient Descent tốt hơn Newton’s method một chút nhưng trên thực tế 2 phương pháp này có độ tốt gần như tương đương nhau. Tuy vậy, người ta vẫn dùng Gradient Descent nhiều hơn so với Newton’s method vì:

• Gradient Descent tốn nhiều lần lặp nhưng một lần lặp thời gian thực hiện ngắn hơn.
• Newton’s method tuy ít lặp hơn nhưng mỗi lần lặp cần thời gian nhiều hơn vì phải tính đạo hàm cấp 2.
• Việc tính đạo hàm là không đơn giản đặc biệt là tính đạo hàm bậc 2 rất phức tạp nên phương pháp Newton ít được lựa chọn.
  Tuy nhiên, nếu số lượng features nhỏ ta dùng Newton’s method sẽ tốt hơn.
  Thông thường nếu số lượng features n <= 1000 thì nên dùng Newton’s method. Nêu n > 1000 thì nên dùng Gradient Descent. Ở đây features có thể xem là số cột của dữ liệu = 2 nên ta dùng Newton’s method việc hội tụ diễn ra nhanh hơn.

Code, Notebook và data có thể tải tại đây.

Tài liệu tham khảo

1. Stanford CS229 Lecture Notes (Notes 1)
2. Machine Learning Cơ bản