Duality

Duality: /dʒuːˈæl.ə.ti/

The Lagrange dual function

The Lagrangian

Xét bài toán sau:

Tìm giá trị x* nhỏ nhất của hàm số \( f_0(x) \) với hàm ràng buộc \(f_1(x)\)

\[ \begin{eqnarray} x^* = \arg\min_x f_0 (x) ~~&(1)& \
s.t: f_1(x) = 0 ~~&(2)& \end{eqnarray} \]

Với \( x = [x_{1}, x_{2}, …, x_{d}] \) d là số chiều của dữ liệu \(x\). Miền xác đinh \( D = dom f_0 \cap dom f_1 \) với \(D \ne \phi\) và hàm mục tiêu và hàm ràng buộc không nhất thiết phải lồi.

Định nghĩa nhân tử lagrange (lagrange multiplier)
Định nghĩa hàm số:
\[ L(x,\lambda)=f_0 (x) + \lambda f_1(x) \] với biến \(\lambda\) gọi là nhân tử lagrange.
Bài toán (1) với ràng buộc (2) có nghiệm là nghiệm của phương trình: \[ \nabla _{x,\lambda} L(x,\lambda) = 0 \] Tương đương với:
\[\nabla _x f_0 (x) + \lambda \nabla _x f_1 (x) = 0 \
f _1 (x) = 0 \]

Phương pháp nhân tử Lagrange cũng được áp cũng nếu bài toán 1 là tìm cực đại.
Ví dụ 1

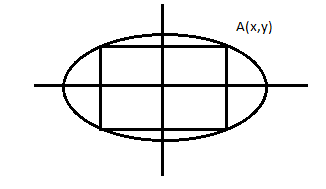
Cho Elip với phương trình: \( E = x^2 + 4 y^2 = 4 \).
Tìm điểm A trên hình sao cho chu vi hình chữ nhật nội tiếp qua A là lớn nhất.

Từ đó, ta suy ra bài toán tối ưu sau:
Với \( P = | 4x + 4y| \) là chu vi hình chữ nhật nội tiếp elip \(E\), Tìm max P.
\[P = |4x + 4y| \
s.t: g(x,y) = x^2 + 4 y^2 = 4 \] \[ \Rightarrow L(x,y,\lambda) = 4x + 4y + \lambda(x^2 + 4 y^2 - 4) \]

Nghiệm của bài toán (7) là nghiệm của phương trình \[ \nabla_{x,y,\lambda} L(x,y,\lambda) = 0 \] Đạo hàm theo các biến \(x,y,\lambda\) ta được hệ: \[4 + \lambda 2 x = 0 \
4 + \lambda 2 y = 0 \
x^2+ 4 y^2 = 4 \] suy ra: \[ x = \pm \frac{4}{\sqrt{5}}\
y = \pm \frac{1}{\sqrt{5}} \]

Lagrangian

Xét bài toán tối ưu tổng quát: \[ x^{*} = \arg \min _{x} f_0(x) ~~ (8)\
\text{subject to: } f_i(x) \leq 0, i = 1, 2, \dots, m \
h_j({x}) = 0, j = 1, 2, \dots, p \]

Với miền xác đinh \(\mathcal{D} = (\cap_{i=0}^m \text{dom}f_i) \cap (\cap_{j=1}^p \text{dom}h_j)\)
Điều kiện: \( \mathcal{D} \neq \emptyset \) , và gia trị tối ưu: p*.

Ta đinh nghĩa Lagrangian \(L: \mathbb{R}^n \text{x} \mathbb{R}^m \text{x}\mathbb{R}^p \rightarrow \mathbb{R} \) . \[ \mathcal{L}({x}, \lambda, \nu) = f_0({x}) + \sum_{i=1}^m \lambda_if_i({x}) + \sum_{j=1}^p \nu_j h_j({x}) \]

Với \( \lambda = [\lambda _1, \lambda _2, \dots, \lambda _m]; \nu = [\nu _1, \nu _2, \dots, \nu _p] \) gọi là dual variables hoặc lagrange multiplier vector.

Hàm đối ngẫu Lagrange

Ta định nghĩa “the Lagrange dual function” \( g: \mathbb{R}^{m} \text{x} \mathbb{R}^{p} \rightarrow \mathbb{R} \) là giá trị nhỏ nhất của Lagrangian trên \( x \).

\[ g(\lambda, \nu) = \inf_{x \in D} \mathcal{L}(x,\lambda,\nu) \
= \inf_{x \in D} \left( f_0(x) + \sum_{i=1}^{m} \lambda_i f_i (x) + \sum_{j=1}^{p} \nu_j h_j (x) \right) \]

Với \(inf\) là Infimum. Khi không bị chặn dưới, dual function mang giá trị \( - \infty \).

Lưu ý: với mỗi x, Lagrange là một hàm affine của \( \lambda,\nu \) (concave) vậy dual function là inf của một hàm concave cũng là một hàm concave.

Chặn dưới của bài toán tối ưu.

Bài toán gốc có giá trị tối ưu p* và \( \lambda _i > 0, \forall i \text{ và } \nu \) bất kỳ. Ta có:
\[ g(\lambda,\nu) \leq p^* ~~ (11) \] Nên \(g(\lambda,\nu) \) gọi là chặn dưới của giá trị tối ưu \(p^*\).
Điều này được chứng minh như sau:
Giả sử \(\hat{x}\) là một điểm feasible thì \( f_i(\hat{x}) \leq 0 \) và \(h_i(\hat{x}) = 0\) và \(\lambda \geq 0\). Tiếp theo ta có \[ \sum _{i=1} ^{m} \lambda _i f_i (\hat{x}) + \sum _{i=1} ^{m} \nu_i h_i (\hat{x}) \leq 0 \]

Vì mỗi phần tử trong tổng thứ nhất \( \leq 0 \) và thứ tổng thứ 2 \( = 0 \) nên:

\[ L( \hat{x}, \lambda, \nu) = f_0 ( \hat{x} ) + \sum _{i=1} ^{m} \lambda _i f_i ( \hat{x} ) + \sum _{i=1} ^{m} \nu_i h_i (\hat{x}) \leq f_0 ( \hat{x} ) \]

\[ g(\lambda,\nu) = \inf_{x \in D} L(x,\lambda,\nu ) \leq L(\hat{x},\lambda,\nu) \leq f_0(\hat{x}) \]

Vì \( g(\lambda,\nu) \leq f_0(\hat{x} ) \) đúng với \( \forall \hat{x} \) feasible.

Bài toán đối ngẫu Lagrange

Với mỗi cặp \( (\lambda , \nu) \) với \( \lambda >0 \). Dual function cho ta một cận dưới của optimal value \( p^* \). Do đó, ta có một cận dưới phụ thuộc vào \( \lambda \text{ và } \nu \) .
Câu hỏi đặt ra là: Tìm giá trị tốt nhất của cận dưới ta thu được từ hàm đối ngẫu lagrange.
Mở đầu cho bài toán:
\[ d^{*} = \text{maximize } g( \lambda, \nu ) ~~ (12) \
\text{s.t: } \lambda \geq 0 \] Bài toán này gọi là “Lagrange dual problem” tương ứng với bài toán (8) (primal problem).

Dual feasible để mô tả cặp \( (\lambda,\nu) \) với \( \lambda \geq 0 \) và \( g(\lambda,\nu) > - \infty \) là feasible set (tập khả thi) của bài toán đối ngẫu.
Ta gọi \( (\lambda *,\nu *) \) là nghiệm của bài toán (12) còn được gọi là dual optimal hoặc optimal Lagrange multipliers.
Đây là một bài toán tối ưu lồi vì hàm muc tiêu là 1 concave và hàm ràng buộc là 1 convex.

Weak duality

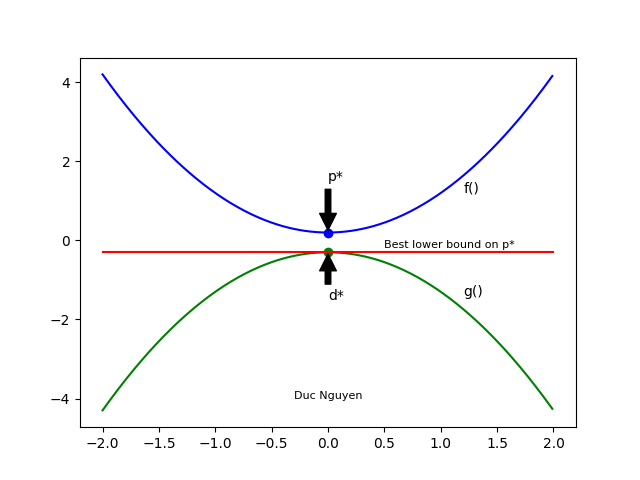
Gọi giá trị tối ưu của bài toán đối ngẫu Lagrange (12) là \( d^* \). ( \( d^* \) được gọi là “best lower bound on p*”). Ta được \[ d^* \leq p^* ~~ (13) \]

Ngay cả khi bài toán gốc không phải là lồi. Thuộc tính này gọi là weak duality.
Hình minh họa:

Strong duality và Slater’s constrain qualification

Nếu dấu “=” tại (13) xảy ra thì đó gọi là strong duality.
Điều này nghĩa là nghiệm tốt nhất của bài toán sẽ tìm được.
Strong duality không thường xuyên xảy ra.
Nếu bài toán gốc (8) là convex tức nó có dạng:
\[ x^* = \arg\min_{x} f_0(x) ~~ (14)\
\text{subject to: } f_i(x) \leq 0, ~~ i = 1, 2, \dots, m \
Ax = b \] Với \( f_0, f_1,…,f_m \) là các hàm lồi thì thường(không phải luôn luôn) có strong duality.
Có những điều kiện ngoài tính chất lồi gọi là constraint qualifications. Một trong những constrain qualifications đơn giản đó là Slater’s condition

Slater’s condition
Tồn tại điểm x có \[ f_i < 0, i = 1,…,m, Ax = b \] Điểm này gọi là strictly feasible.
Định lý Slater: nếu tồn tại một điểm strictly feasible (và bài toán gốc là lồi) thì strong duality xảy ra.
Chú ý:

• Strong duality không thường xảy ra, với bài toán lồi. Với bài toán lồi, điều này thường xảy ra hơn.

Complementary slackness (Bù yếu)

Giả sử rằng strong duality xảy ra. Gọi \( x^* \) là điểm optimal của bài toán gốc và \( ( \lambda^* , \nu^* ) \) điểm optimal của bài toán đối ngẫu. Điều đó có nghĩa là:
\[ \begin{eqnarray} f_0( x^{*} ) &=& g(\lambda^{*} , \nu^{*}) \
&=& \inf_x \left( f_0 ( x ) + \sum_{i=1}^{m} {\lambda_i^{*} f_i(x)} + \sum_{j=1}^{p}{\nu_j^{*}h_i(x)} \right) \\
&\leq& f_0( x^{*}) + \sum_{i=1}^{m} {\lambda_i^{*} f_i (x)} + \sum_{j=1}^{p}{\nu _j ^{*} h _i (x)} \
&\leq& f_0 ( x^{*}) \end{eqnarray} \]

• Dòng đầu là do strong duality
• Dòng thứ 2 là định nghĩa hàm đối ngẫu
• Dòng thứ 3 là vì infimum
• Dòng thứ 4 là vì \( f_i( x^* ) \leq 0, \lambda_i \geq 0, i= 1,2,…,m \text{ và } h_j ( x^*) =0 \).

Từ đó ta suy ra \[\sum_{i=1}^{m} {\lambda_i^{*} f_i(x)} =0 \] với \( x^* \) là giá trị nhỏ nhất của \( L( x, \lambda^{*}, \nu^{*}) \) và vì mỗi phần tử trên tổng không âm nên ta suy ra tiếp \[ {\lambda_i^{*} f_i(x)} =0 , ~~ i = 1, \dots, m \] Điều kiện này gọi là Complementary slackness.

KKT optimality conditions

Giả sử \( f_0, f_1, …, f_m, h_0, …, h_p \) khác nhau (và có miền xác đinh). Ta không giả sử nó lồi.
Đối với bài toán không lồi

Giả sử cho \( x^{*} \) và \( (\lambda ^{*} , \nu^{*}) \) là bất kỳ primal và dual optimal point
Vì tại \( x^{*} \text{, } L(x,\lambda^{*},\nu^{*}) \) có giá trị nhỏ nhất nên đạo hàm tại \( x^{*} = 0\).
\[ \nabla f_0(x^{*}) + \sum_{i=1}^{m}{\lambda_i^{*} \nabla f_i(x)} + \sum_{j=1}^{p}{\nu_j^{*} \nabla h_i } \] Từ đó ta có điều kiện Karush-Kuhn-Tucker (KKT):
Với \( x^{*}, \lambda^{*}, \nu^{*}\)

\[ \begin{eqnarray} f_i({x}^{*}) &\leq& 0, ~~ i = 1, 2, \dots, m \\
h_j({x}^{*}) &=& 0, ~~ j = 1, 2, \dots, p \\
\lambda_i^{*} &\geq& 0, ~~ i = 1, 2, \dots, m \\
\lambda_i^{*}f_i({x}^{*}) &=& 0, ~~ i = 1, 2, \dots, m \\
\nabla f_0({x}^{*}) + \sum_{i=1}^m \lambda_i^{*} \nabla f_i({x}^{*}) + \sum_{j=1}^p\nu_j^{*} \nabla h_j({x}^{*}) &=& 0 \end{eqnarray} \]
Đây là điều kiện cần để \( x^{*}, \lambda^{*}, \nu^{*} \) là nghiệm của bài toán.

Đối với bài toán lồi
Với bài toán lồi và điều kiện Slater thỏa mãn (suy ra strong duality) thì các điều kiện KKT là điều kiện cần và đủ của nghiệm.

Tóm tắt:
Updating… \[…\]

Support vector machine

Giới thiệu

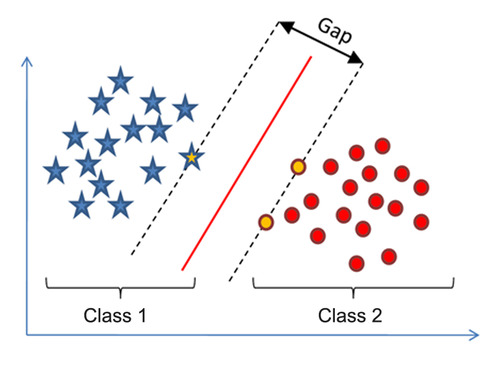
Trong không gian 2 chiều trên, ta cần tìm một đường phân loại 2 class sao cho 2 class nằm về 2 phía của đường phân loại, khoảng cách từ 1 phần từ bất kỳ đến đường phân loại là lớn nhất.
Bài toán tối ưu này gọi là Support vector machine (SVM).

Xây dựng bài toán

Ta có tập huấn luyện (training set) là \( {(x_1,y_1),(x_2,y_2),\dots,(x_N,y_N)} \) với vector \( x_i = [x_{i1},x_{i1},\dots,x_{iD}]^T \) với N là số lượng điểm dữ liệu và D là số chiều của dữ liệu.
Giả sử rằng \( y_i \in \{ -1, 1 \}, \forall i \) với \( y_i = 1 \) tương ứng với class 1 và \( y_i = -1 \) tương ứng với class 2.
Giả sử: \[ \hat{y}(x_i, w, b) = w^T x_i + b = w_{1}x_{i1} + w_{2}x_{i2} + \dots + w_{D}x_{iD} + b = 0 ~~ (15)\] là mặt phân cách. Class 1 nằm về phía dương và class 2 nằm về phía âm của \( \hat{y} \).
Khoảng cách từ một điểm đến tới mặt phân cách \( \hat{y} \) là: \[ \frac{sgn(w^Tx_i+b )(w^Tx_i+b )}{||{w}||_2} = \frac{y_i(w^Tx_i+b ) }{||{w}||_2} ~~ (16) \]

Margin được tính là khoảng cách gần nhất từ 1 điểm tới mặt đó. \[ margin = \min_{i } \frac{y_i(w^Tx_i+b ) }{||{w}||_2} ~~ (17) \]

Bài toán tối ưu trong SVM là bài toán tìm w và b sao cho margin đạt giá trị lớn nhất.

\[ (w^{*},b^{*}) = \arg \max _{(w,b)} \left( \frac{y_i(w^Tx_i+b ) }{||{w}||_2} \right) \\
= \arg \max _{(w,b)} \left( \frac{1 }{||{w}||_2} \min _{i} y_i(w^Tx_i+b) \right) ~~ (18) \]

Vì w và b là 2 biến số nên ta giả sử \( y_i(w^Tx_i+b) \geq 1 \).
Ta đưa bài toán (18) thành bài toán tôi ưu có ràng buộc: \[ (w^{*},b^{*}) = \arg \max _{(w,b)} \left( \frac{1 }{||{w}||_2} \right) \\
\text{s.t: } y_i(w^Tx_i+b) \geq 1, \forall i = 1,2, \dots , N ~~ (19) \] Biến đổi bài toán thành:
\[ (w^{*},b^{*}) = \arg \min _{(w,b)} \frac{1 }{2} {||{w}||_2^2} \\
\text{s.t: } 1 - y_i(w^Tx_i+b) \leq 0, \forall i = 1,2, \dots , N ~~ (20) \] Ta có hàm mục tiêu có dạng hàm toàn phương là một hàm lồi và hàm ràng buộc cũng là các hàm lồi nên nó là một bài toán tối ưu lồi, thập chí vì hàm mục tiêu lồi hoàn toàn (strictly convex) nên nghiệm là duy nhất.
Để xác định class cho một điểm sau khi tìm được mặt phân cách \( \hat{y} \) ta sử dụng công thức: \[ class(x) = sgn(\hat{y}(x)) ~~ (21) \]

Giải bài toán

Kiểm tra chuẩn Slater
Điều kiện Slater: nếu tồn tại w,b sao thỏa \[ 1- y_i (w^T x_i +b ) < 0 , \forall i = 1,2, \dots , N ~~ (22) \] thì Strong duality thỏa. Chứng minh: luôn tồn tại \( w_0, b_0 \) sao cho \[ 1- y_i ( w_0^T x_i + b_0 ) \leq 0, \forall i = 1,2, \dots, N ~~ (23) \
\Leftrightarrow 2- y_i ( 2w_0^T x_i + 2b_0 ) \leq 0, \forall i = 1,2, \dots, N ~~ (23) \] Chọn \( w_1 = 2w_0 \text{ và } b_1 = 2b_0 \) ta sẽ có: \[ 1- y_i ( w_1^T x_i + b_1 ) \leq -1 < 0, \forall i = 1,2, \dots, N ~~ (25) \] Vậy nên thỏa chuẩn Slater.

Lagrangian của bài toán

Ta có có Lagrangian của bài toán:

\[ L(w,b,\lambda) = \frac{1}{2}{||w||_2^2} + \sum _{i=1}^{N} \lambda _{i} (1 - y_i (w^T x_i + b )) ~~ (26) \]

Với \( \lambda = [\lambda_1,…,\lambda_N]^T \text{ và } \lambda _i \geq 0, \forall i = 1,2,…,N \)

Hàm đối ngẫu lagrange
Hàm đối ngẫu của bài toán là: \[ g( \lambda ) = \inf _ {( w, b )} L(w, b, \lambda ) = \min _ {( w, b)} L(w, b, \lambda ) ~~ (27) \] Với \( \lambda \geq 0 \). Ta có thể giải vế phải bằng cách giải hệ phương trình gradient của \( L(w, b, \lambda ) \) theo w và b bằng 0.
Giải bài toán \( \nabla _ {( w, b)} g( \lambda ) = 0 \) ta suy ra hệ:

\[ \frac { \partial L (w, b, \lambda ) }{ \partial w } = w - \sum _ {i=1}^{N} \lambda _i y_i x_i = 0 \\
\Rightarrow w = \sum _ {i=1} ^ {N} \lambda _i y_i x_i ~~ (28) \\
\frac { \partial L (w,b, \lambda ) }{ \partial b } = \sum _ {j=1}^{N} \lambda _j y_j = 0 ~~ (29) \]

Thay kết quả trên vào \( g( \lambda ) \) ta được nghiệm

\[ g( \lambda ) = \sum _ {i=1}^{N} \lambda _i - \frac {1}{2} \sum _ {j = 1} ^{N} \sum _{k = 1} ^{N} \lambda _j \lambda _k y_j y_k x_j^T x_k ~~ (30) \]

Bài toán đối ngẫu Bài toán đối ngẫu của (26) như sau: \[ \lambda ^ {*} = \arg \max _ {\lambda } g(\lambda ) ~~ (31) \\
\text{ s.t: } \lambda \geq 0 ~~ (32) \\
\sum _ {i=1}^{N} \lambda _i y_i = 0 ~~ (33) \] Ràng buộc (33) được lấy từ (29).
Điều kiện KKT
Đây là bài toán lồi và đã thỏa strong duality nên nghiệm của bài toán thỏa hệ điều kiện KKT sau đây với biến là w, b và \( \lambda \): \[ \begin{eqnarray} 1 - y_i ( w^Tx_i + b) &\leq& 0 , \forall i = 1, 2, \dots , N ~~ (34) \\
\lambda _i &\geq& 0 , \forall i = 1, 2, \dots , N \\
\lambda _i ( 1 -y_i (w^T x_i +b ) ) &=& 0 , \forall i = 1, 2, \dots , N ~~ (35) \\
w &=& \sum _ {i=1} ^{ N} \lambda _i y_i x_i ~~ ~~ (36) \\
\sum _ {i =1 } ^{N} \lambda _i y_i &=& 0 ~~ ~~ ~~ (37) \end{eqnarray} \]

Giải (35) ta được 2 trường hợp \( \lambda _i = 0 \) hoặc \( 1 -y_i (w^T x_i +b ) = 0 \).
Trong trường hợp thứ 2 ta suy ra: \[ y_i y_i (w^Tx_i + b ) = y_i \Leftrightarrow w^Tx_i + b = y_i ~~ (38) \]

Trường hợp này chính là những điểm nằm trên đường thẳng \( \hat{y} = \pm 1 \).
Những điểm (hay vector) này còn được gọi là giá vector (support vector).

Tiếp theo, ta gọi \( S = \{ n | \lambda _n \neq 0 \} \text{ và } N_S \) là số phần tử của S. Với mỗi điểm \( x_s \in S \) ta có: \[ 1 = y_s(w^Tx_s + b) \Leftrightarrow b = y_s = w^T x_s ~~ (39) \] Ta cũng có thể tính trung bình của b đối với mỗi \( x_s \) để tăng tính chắc chắn. \[ b = \frac {1}{N_S} \sum _ {s \in S} (y_s - w^Tx_s) = \frac {1}{N_S} \sum _ {s \in S} (y_s - \sum _ {t \in S} \lambda _s y_s x_t^T x_s) ~~ (40) \]

Vậy là ta đã tính được b. Trước đó ta có \[ w = \sum _ {i=1} ^{N} \lambda _i y_i x_i ~~ (41) \] ta thay w bà b vừa được tính vào mặt phân cách \( \hat{y} \) ta được \[ \hat{y} = w^Tx + b = \sum _ {t \in S} \lambda _t y_t x_t^T x + \frac {1}{N_S} \sum _ {s \in S} ( y_s - \sum _ {t \in S} \lambda _s y_s x_t^T x_s ) ~~ (42) \]

Hiện thực SVM

Ta sẽ sử dụng thư viện scikit-learn trong python để hiện thực cách lập trình nghiệm cho bài toán SVM.

import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm
import random

# y = 2x - 1
# Generating data
X = np.array([i/10. + random.random()/2. for i in range(-10,10)])
Y1 = 2*X - 1 + 2
Y2 = 2*X - 1 - 2
for i in range(len(Y1)):
	Y1[i] = Y1[i] + random.random()
	Y2[i] = Y2[i] + random.random()
Xdata = []
Ydata = []
for i in range(len(X)):
	Xdata.append([X[i], Y1[i]])
	Xdata.append([X[i], Y2[i]])
	Ydata.append(0)
	Ydata.append(1)

Xdata = np.array(Xdata)
Ydata = np.array(Ydata)


clf = svm.SVC(kernel = 'linear', C = 1e6)
clf.fit(Xdata,Ydata)

# Print support vectors
print clf.support_vectors_
print
# Print w and b
w = clf.coef_
b = clf.intercept_
print w , b


# Plot data
for i in range(len(X)):
	plt.plot(X[i],Y1[i],'ro')
for i in range(len(X)):
	plt.plot(X[i],Y2[i],'bo')

# Plot classification line
Xline = np.array([-1.2, 2])
Yline = -1*Xline * w[0][0]/w[0][1] - b[0]/w[0][1]
plt.plot(Xline,Yline)

plt.show()

Kết quả support vectors và w, b như sau:

[[-0.65991059 -0.22613997]
 [-0.30739343 -2.61819165]
 [ 1.05506403  0.02238899]]

[[ 1.26003173 -0.65013722]] [-0.31507677]

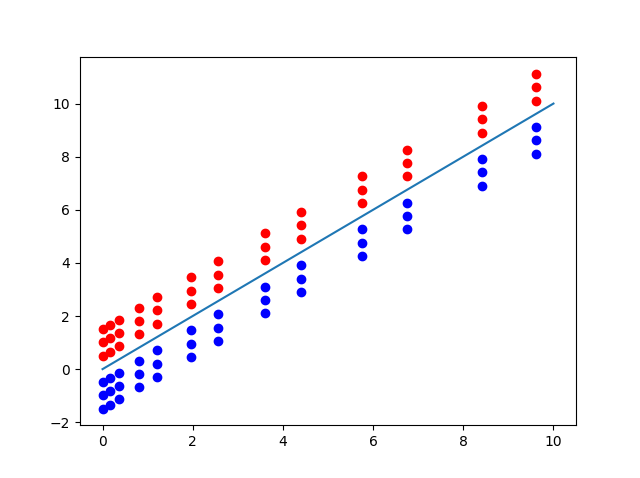
Dữ liệu và đường phân loại được plot ra như hình.

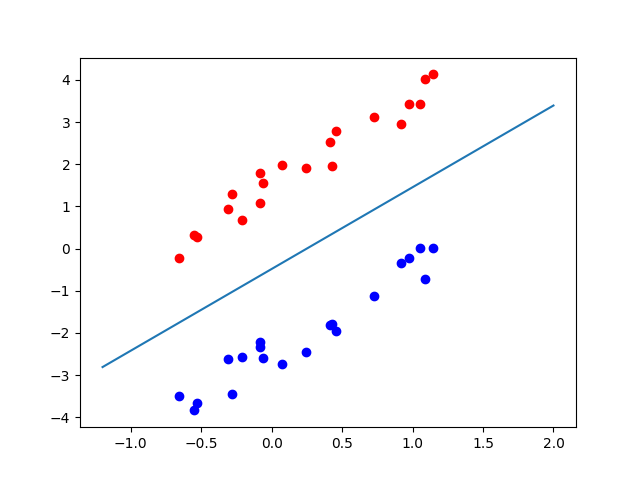
Chú ý : dữ liệu được sinh ngẫu nhiên nên kết quả mỗi lần thực hiện sẽ khác nhau.

Soft Margin - SVM

Bài toán phân loại 2 class ở trên 2 class được phân loại rõ ràng nhưng nếu 2 class có lẫn lộn nhau 1 phần hoặc có nhiễu (Như hình minh họa bên dưới) thì thuật toán sẽ không thực hiện được.
Từ đó người ta phát triển phương pháp ban đầu (hard margin) thành một phương pháp mới bỏ qua một số điểm cho vào vùng không an toàn. Phương pháp đó gọi là soft margin.

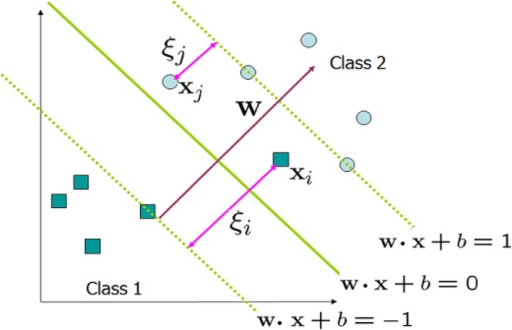
Soft margin sẽ là dạng tổng quát của hard margin.
Về cách xây dựng bài toán tương tự như với phần hard margin nên ta sẽ trình bay nhanh qua phần này. —

Bài toán soft margin tổng quát

Ta gọi \( \xi \) là giá trị đại diện cho các điểm phân loại không đúng \( ( \xi > 1) \) hoặc nằm trong vùng margin \( ( 0 < \xi < 1 ) \). Bài toán soft margin SVM có dạng như sau:
\[ (w,b, \xi ) = \arg \min _ {w,b, \xi } \frac {1}{2} ||w||^2_2 +C \sum _ {i =1}^{N} \xi _i ~~ (43) \
s.t: 1 - \xi _i - y_i (w^Tx_i +b) \leq 0, \forall i = 1,2,…,N ~~ (44) \
-\xi _i \leq 0, \forall i = 1,2,…,N \]

Với C là một hằng số dương và \( \xi = [ \xi _1 , \xi _2 , \dots, \xi _ N ]^T \)

Tiêu chuẩn Slater cho soft margin

Theo đề bài ta có: \[ 1-\xi _i - y_i(w^Tx_i +b) \leq 0 \
\Leftrightarrow 1 \geq \xi _i + y_i(w^Tx_i +b) \
\Leftrightarrow \xi _i + y_i(w^Tx_i +b) > 0 \
\] Vậy bài toán thỏa tiêu chuẩn Slater

Lagrangian của bài toán soft margin

Ta xây dựng được Lagrangian như sau \[ L(w,b, \xi , \lambda , \mu ) = \frac {1}{2} ||w||^2_2 + C \sum _ {i=1}^{N} \xi _i + \sum _ {i=1}^{N} \lambda _ i (1- \xi _i-y_i(w^Tx_i+b))- \sum _ {i=1}^{N} \mu _i \xi _i ~~ (45) \] Với \( \lambda = [ \lambda _1, \lambda _2,…, \lambda _N]^T \succeq 0 \text{ và } \mu = [ \mu _1, \mu 2,…, \mu _N]^T \succeq 0 \) là các biến đối ngẫu Lagrange.

Bài toán đối ngẫu

Hàm đối ngẫu của bài toán như sau: \[ g( \lambda , \mu ) = \min _ {(w,b, \xi )} L(w,b, \xi , \lambda , \mu ) ~~ (46) \]

Tương tự với bài toán hard margin, Giá trị nhỏ nhất của vế phải đạt được tại điểm có đạo hàm của \( L(w,b, \xi , \lambda , \mu ) = 0 \). Ta có hệ phương trình: \[ \frac { \partial L}{ \partial w} = 0 \Leftrightarrow w = \sum _ {i=1}^{N} \lambda _i y_i x_i ~~ (47) \
\frac { \partial L}{ \partial b} = 0 \Leftrightarrow \sum _ {i=1}^{N} \lambda _i y_i =0 ~~ (48) \
\frac { \partial L}{ \partial \xi _i} = 0 \Leftrightarrow \lambda _i = C - \mu _ i ~~ (49) \]

Từ (49) ta suy ra \( 0 \leq \lambda _i, \mu _i \leq C, i = 1,2,…,N \).

Thay các biểu thức trên vào Lagrangian ta suy ra hàm số đối ngẫu: \[ g( \lambda , \mu) = \sum _ {i=1}^{N} \lambda _i - \frac {1}{2} \sum _ {i=1}^{N} \sum _ {j=1}^{N} \lambda _ i \lambda _ j y_i y_j x_i^T x_j ~~ (50) \]

Từ đó ta có được bài toán đối ngẫu: \[ g( \lambda , \mu ) = \sum _ {i=1}^{N} \lambda _i - \frac {1}{2} \sum _ {i=1}^{N} \sum _ {j=1}^{N} \lambda _ i \lambda _j y_i y_j x_i^Tx_j ~~ (51) \
\text {subject to: } \sum _ {i=1}^{N} \lambda _i y_i ~~ (52) \
0 \leq \lambda _i \leq C , \forall i = 1,2,…,N ~~ (53) \]

Điều kiên KKT cho bài toán soft margin

\[ \begin{eqnarray} 1 - \xi _i - y_i ( w^T x_i + b) &\leq& 0 ~~ (54) \
- \xi _i &\leq& 0 ~~ (55) \
\lambda _i &\geq& 0 ~~ (56) \
\mu _i &\geq& 0 ~~ (57) \
\lambda _i (1- \xi _i - y_i (w^T x_i +b)) &\leq& 0 ~~ (58) \
\mu _i \xi _i &=& 0 ~~ (59) \
w &=& \sum _ {i=1}^{N} \lambda _i y_i x_i ~~ (60) \
\sum _ {i=1}^{N} \lambda _i y_i &=& 0 \
\lambda _i &=& C - \mu _i \end{eqnarray} \]

Nếu \( \lambda _i = 0 \) suy ra \( \mu _ i = C \) suy ra \( \xi _i =0 \) nghĩa là không có điểm nào phải bỏ qua.
Nếu \( \lambda _i > 0 \) suy ra \[ 1- \xi _i = y _i (w^T x_i + b ) \] Nếu \( 0 < \lambda _i < C \) suy ra \( \mu _i \ne 0 \) suy ra \( \xi _i = 0 \) tương đương với \( y_i (w^T x_i + b) = 1 \) ( các điểm \( x_i \) nằm trên margin).

Với những điểm \( \lambda _i >0 \) sẽ là các support vector.
Đặt \( M = \{ n | 0 < \lambda _n < C \} \text{ và } S = \{m | 0 < \lambda _m \} \). Suy ra được b và w: \[ w = \sum _ {m \in S} \lambda _ m y _ m x _ m \
b = \frac {1} {N_M} \sum _ {n \in M} {(y_n - w^T x)} = \frac {1}{N_M} \sum _ {n \in M} \left( y_n - \sum _ {m \in S} \lambda _m y_m x^T _m x_n \right) \] Thế vào \( w^T x + b \) ta được: \[ w^T x + b = \sum _ { m \in S} \lambda _ m y _ m x^T _m x + \frac {1}{N_M} \sum _ {n \in M} \left( y_n - \sum _ {m \in S} \lambda _ m y _m x^T_m x_n \right) \]

Hiện thực soft margin

Ta sẽ hiện thực với tập dữ liệu ex4 giống bài Logistic Regression

# Import sklearn
from sklearn import svm
# Readfile
fx = open("ex4x.dat").read().strip().split('\n');

X = []
y = []

for i in fx:
    tmp = i.split()
    X.append( [ float(tmp[0]) ,float(tmp[1]) ] )
fy = open("ex4y.dat").read().split('\n');
for i in fy[:-1]:
    y.append(float(i))

clf = svm.SVC(kernel = 'linear'); # Using soft margin
clf.fit(X,y);
w = clf.coef_
b = clf.intercept_
print w,b

from matplotlib import pyplot as plt
import numpy as np
X0 = [X[x0][0] for x0 in range(40)]
X1 = [X[x1][1] for x1 in range(40)]
X2 = [X[x2][0] for x2 in range(40,80)]
X3 = [X[x3][1] for x3 in range(40,80)]
plt.plot( X0, X1, "r+")
plt.plot( X2, X3, "bo")
plt.xlabel('Diem 1')
plt.ylabel('Diem 2')


pltx = [15,65];
w0 = w[0][0]
w1 = w[0][1]
plty = [];
plty.append((-1. / w1) * ( w0 * pltx[0] +b[0]));
plty.append((-1. / w1) * ( w0 * pltx[1] +b[0]));
plt.plot(pltx, plty)
plt.show()

Output như sau:

[[ 0.10918793  0.12291274]] [-12.51099492]

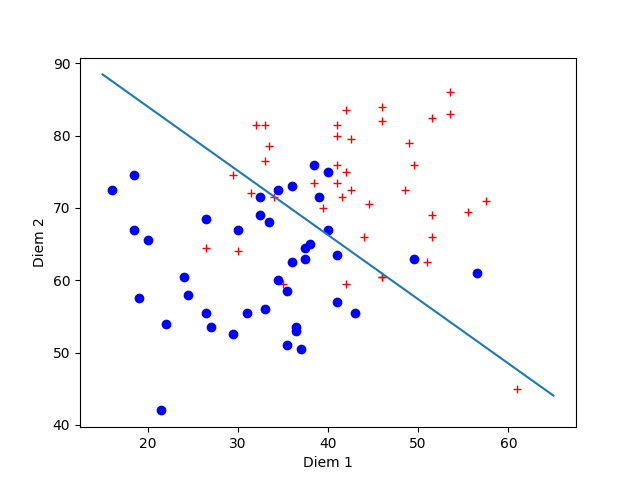
Kernel SVM

Soft margin đã giải quyết được vấn đề của 2 class phân loại không hoàn toàn hoặc có nhiễu thế nhưng nó chỉ phân loại tuyến tính (đường phân loại có dạng \( Ax + b = 0 \) ). Đối với dữ liệu phân loại không tuyến tính, soft margin cũng sẽ gặp thất bại ngay.
Hình bên dưới cho thấy sự thất bại của soft margin trong một trường hợp dữ liệu phân loại không tuyến tính.

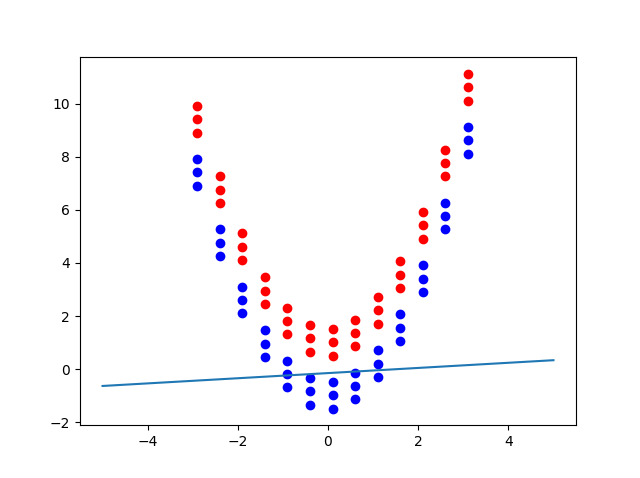
Nhưng nếu chuyển dữ liệu trên vào một không gian mới từ \( (x_1, x_2) \text{ đến } (x_1^2, x_2) \) thì dữ mới trở thành như hình dưới:

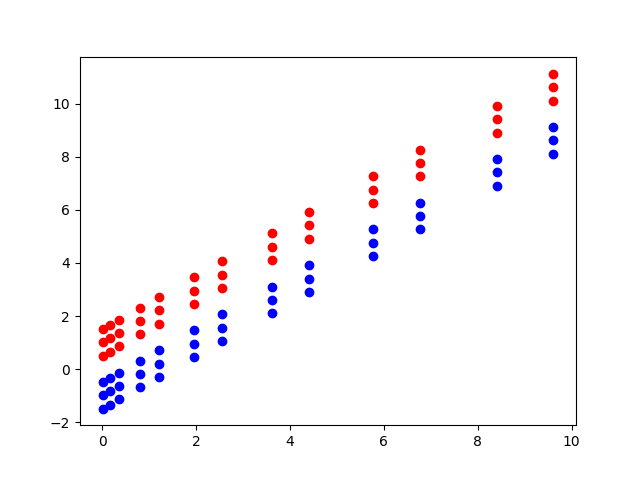
Ta thấy lúc này dữ liệu đã được phân loại tuyến tính. Ta chỉ cần áp dụng soft margin hoặc các phương pháp phân loại tuyến tính khác đối với bài dữ liệu mới này.

Q: Vậy là đã giải quyết được bài toán trên rồi sao?

A: Đúng vậy!

Q: Nhưng vì sao có thể biết được chuyển sang không gian từ \( (x_1, x_2) \text{ đến } (x_1^2, x_2) \) thì dữ liệu sẽ về dạng tuyến tính.

A: Vì khi plot dữ liệu lên ta có thể thấy được chúng phân loại bằng một đường cong dạng Parabol nên sử dụng không gian mới đó.

Q: Với những bài toán khác thì sao? nếu dữ liệu có dạng đường cong phức tạp hoặc nhiều hơn 3 chiều thì việc phân loại và đoán phép biến đổi không gian như trên có còn khả thi không?

A: Việc hiện thị dữ liệu như trên gọi là Data visualization đây là một kỹ thuật đang được phát triển trong khoa học dữ liệu. Có những kỹ thuật hiển thị giúp ta dễ hình dung cũng như tìm ra được những phương pháp xử lý cho bài toán của ta. Thế nhưng không phải dữ liệu nào cũng có thể hiện thị được nên đây cũng là một kỹ thuật còn đang được phát triển. Nếu dữ liệu phức tạp thì đây không phải là cách khả thi để giải quyết bài toán như trên.

Q: Vậy có cách nào khác không?

A: Có! Kernel.

Kernel

Trên ý tưởng đó, ta sẽ biến đổi không gian ban đầu thành không gian mới sử dụng hàm \( \Phi (x) \). Đối với ví dụ trên, \( \Phi (x) = [x_1^2 , x_2]^T \).
Trong không gian mới, bài toán trở thành:

\[ \lambda ^{*} = \arg \max _ { \lambda } \sum _ {i=1}^{N} \lambda _i - \frac {1}{2} \sum _ {i=1}^{N} \sum _ {j=1}^{N} \lambda _ i \lambda _j y_i y_j \Phi (x_i)^T \Phi (x_j) \
\text {subject to: } \sum _ {i=1}^{N} \lambda _i y_i \
0 \leq \lambda _i \leq C , \forall i = 1,2,…,N
\] \[ f( \Phi (x) ) = w^T \Phi (x) + b = \sum _ {m \in S} \lambda _ m y _ m \Phi (x_m)^T \Phi (x) + \frac {1}{N_M} \sum _ {n \in M} \left( y_n - \sum _ {m \in S} \lambda _ m y_m \Phi (x_m)^T \Phi (x_n) \right) \]

Để tính được \( \Phi (x) \) là công việc rất khó, thậm chí \( \Phi (x) \) có thể có số chiều rất lớn.
Quan sát các biểu thức trên ta thấy, thay vì tính \( \Phi (x)\), ta chỉ cần tính \( \Phi (x)^T \Phi (z) \) với 2 điểm \( x,z \) bất kỳ.
Kỹ thuật này gọi là kernel trick.
Phương pháp dùng kỹ thuật này gọi là kernel method.

Định nghĩa hàm kernel \( k(x,z) = \Phi (x)^T \Phi (z) \) Ta viết lại bài toán thành:

\[ \lambda ^{*} = \arg \max _ { \lambda } \sum _ {i=1}^{N} \lambda _i - \frac {1}{2} \sum _ {i=1}^{N} \sum _ {j=1}^{N} \lambda _ i \lambda _j y_i y_j k(x_i , x_j ) \
\text {subject to: } \sum _ {i=1}^{N} \lambda _i y_i \
0 \leq \lambda _i \leq C , \forall i = 1,2,…,N
\] \[ f( \Phi (x) ) = w^T \Phi (x) + b = \sum _ {m \in S} \lambda _ m y _ m k(x_m , x) + \frac {1}{N_M} \sum _ {n \in M} \left( y_n - \sum _ {m \in S} \lambda _ m y_m k(x_m , x_n) \right) \]

Tính hàm kernel

Xét phép biến đổi không gian 2 chiều \( x = [x_1,x_2]^T \) thành không gian 5 chiều \( \Phi (x) = [1, \sqrt {2}x_1, \sqrt {2}x_2, x_1^2, \sqrt {2}x_1x_2, x_2^2 ]^T \). Ta có: \[ k(x,z) = \Phi (x)^T \Phi (z) \
= [1, \sqrt {2}x_1, \sqrt {2}x_2, x_1^2, \sqrt {2} x_1 x_2 , x_2^2 ] [1, \sqrt {2} z_1 , \sqrt {2} z_2 , z_1^2 , \sqrt {2} z_1 z_2 , z_2^2 ]^T \
= 1 + 2x_1z_1 + 2 x_2 z_2 + x_1^2z_1^2 + 2 x_1x_2z_1z_2 + x_2^2 z_2^2 \
= (1+x_1z_1 + x_2z_2)^2 \
= (1+ x^Tz)^2 \]

Từ đó ta thấy việc tính kernel \(k()\) với 2 điểm dữ liệu dễ dàng hơn việc tính từng \(\Phi(x)\) rồi nhân với nhau.

Tính chất của hàm kernel

Hàm kernel thường phải thỏa Mercer’s theorem:
Cho tập dữ liệu \( x_1,…,x_n \) và tập các số thực bất kỳ \( \lambda _1, \dots , \lambda _n \). Hàm \( K() \) phải thỏa: \[ \sum _ {i=1}^{n} \sum _ {j=1} ^ {n} \lambda _ i \lambda _ j K(x_i,x_j) \geq 0 \] Điều này có nghĩa là hàm mục tiêu là các hàm lồi.
Trên thực tế cũng có một số hàm mục tiêu không thỏa Mercer’s theorem nhưng vẫn được dùng làm kernel vì kết quả chấp nhận được.

Các hàm kernel thông dụng

Trên thực nghiệm, người ta thường sử dụng các hàm kernel thông dụng sau:

• Linear: \[ k(x,z) = x^Tz \]
• Polynomial: \[ k(x,z) = (r + \lambda x^Tz)^d \] Với d là số dương chỉ bật của đa thức.
• Radial Basic Function \[ k(x,z) = exp ( - \lambda ||x-z|| _ 2^2), \lambda >0 \]
• Sigmoid: \[ k(x,z) = tanh (r+ \lambda x^Tz) \]

Hiện thực kernel SVM

Ta sẽ sử dụng tập dữ liệu trên để hiện thực việc phân loại bằng kernel SVM

import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm

# Dataset
X = np.c_[( -2.9 , 8.91 ),
        ( -2.4 , 6.26 ),
        ( -1.9 , 4.11 ),
        ( -1.4 , 2.46 ),
        ( -0.9 , 1.31 ),
        ( -0.4 , 0.66 ),
        ( 0.1 , 0.51 ),
        ( 0.6 , 0.86 ),
        ( 1.1 , 1.71 ),
        ( 1.6 , 3.06 ),
        ( 2.1 , 4.91 ),
        ( 2.6 , 7.26 ),
        ( 3.1 , 10.11 ),
        ( -2.9 , 9.41 ),
        ( -2.4 , 6.76 ),
        ( -1.9 , 4.61 ),
        ( -1.4 , 2.96 ),
        ( -0.9 , 1.81 ),
        ( -0.4 , 1.16 ),
        ( 0.1 , 1.01 ),
        ( 0.6 , 1.36 ),
        ( 1.1 , 2.21 ),
        ( 1.6 , 3.56 ),
        ( 2.1 , 5.41 ),
        ( 2.6 , 7.76 ),
        ( 3.1 , 10.61 ),
        ( -2.9 , 9.91 ),
        ( -2.4 , 7.26 ),
        ( -1.9 , 5.11 ),
        ( -1.4 , 3.46 ),
        ( -0.9 , 2.31 ),
        ( -0.4 , 1.66 ),
        ( 0.1 , 1.51 ),
        ( 0.6 , 1.86 ),
        ( 1.1 , 2.71 ),
        ( 1.6 , 4.06 ),
        ( 2.1 , 5.91 ),
        ( 2.6 , 8.26 ),
        ( 3.1 , 11.11 ),
        ( -2.9 , 7.91 ),
        ( -2.4 , 5.26 ),
        ( -1.9 , 3.11 ),
        ( -1.4 , 1.46 ),
        ( -0.9 , 0.31 ),
        ( -0.4 , -0.34 ),
        ( 0.1 , -0.49 ),
        ( 0.6 , -0.14 ),
        ( 1.1 , 0.71 ),
        ( 1.6 , 2.06 ),
        ( 2.1 , 3.91 ),
        ( 2.6 , 6.26 ),
        ( 3.1 , 9.11 ),
        ( -2.9 , 7.41 ),
        ( -2.4 , 4.76 ),
        ( -1.9 , 2.61 ),
        ( -1.4 , 0.96 ),
        ( -0.9 , -0.19 ),
        ( -0.4 , -0.84 ),
        ( 0.1 , -0.99 ),
        ( 0.6 , -0.64 ),
        ( 1.1 , 0.21 ),
        ( 1.6 , 1.56 ),
        ( 2.1 , 3.41 ),
        ( 2.6 , 5.76 ),
        ( 3.1 , 8.61 ),
        ( -2.9 , 6.91 ),
        ( -2.4 , 4.26 ),
        ( -1.9 , 2.11 ),
        ( -1.4 , 0.46 ),
        ( -0.9 , -0.69 ),
        ( -0.4 , -1.34 ),
        ( 0.1 , -1.49 ),
        ( 0.6 , -1.14 ),
        ( 1.1 , -0.29 ),
        ( 1.6 , 1.06 ),
        ( 2.1 , 2.91 ),
        ( 2.6 , 5.26 ),
        ( 3.1 , 8.11 )
].T

ln = len(X)
r = ln/2
Y = [0] * r + [1] * r
# figure number
fignum = 1

# fit the model
for kernel in ('sigmoid', 'poly', 'rbf'):
    clf = svm.SVC(kernel=kernel, gamma=5, coef0 = 1, degree = 2)
    clf.fit(X, Y)
    if True:
        # plot the line, the points, and the nearest vectors to the plane
        fig, ax = plt.subplots()
        plt.figure(fignum, figsize=(4, 3))
        plt.clf()
        plt.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], s=80,
                    facecolors='None')
        plt.plot(X[:r, 0], X[:r, 1], 'ro', markersize = 6)
        plt.plot(X[r:, 0], X[r:, 1], 'bs', markersize = 6)
        plt.axis('tight')
        x_min, x_max = -5, 5
        y_min, y_max = -3, 12
        XX, YY = np.mgrid[x_min:x_max:200j, y_min:y_max:200j]
        Z = clf.decision_function(np.c_[XX.ravel(), YY.ravel()])
        # Put the result into a color plot
        Z = Z.reshape(XX.shape)
        plt.figure(fignum, figsize=(4, 3))
        CS = plt.contourf(XX, YY, np.sign(Z), 200, cmap='jet', alpha = .2)
        plt.contour(XX, YY, Z, colors=['k', 'k', 'k'], linestyles=['--', '-', '--'],
                    levels=[-.5, 0, .5])
        plt.title(kernel, fontsize = 15)
        plt.xlim(x_min, x_max)
        plt.ylim(y_min, y_max)
        plt.xticks(())
        plt.yticks(())
        fignum = fignum + 1
        #pdf.savefig()
        #plt.show()
plt.show()

# Reference from blog: Machinelearningcoban

Kết quả được hiển thi như sau:

• Radial Basic Function (rbf) :

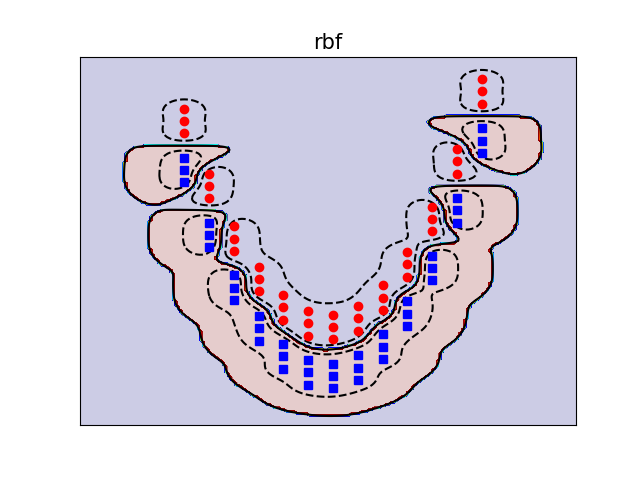
• Polynomial (poly):

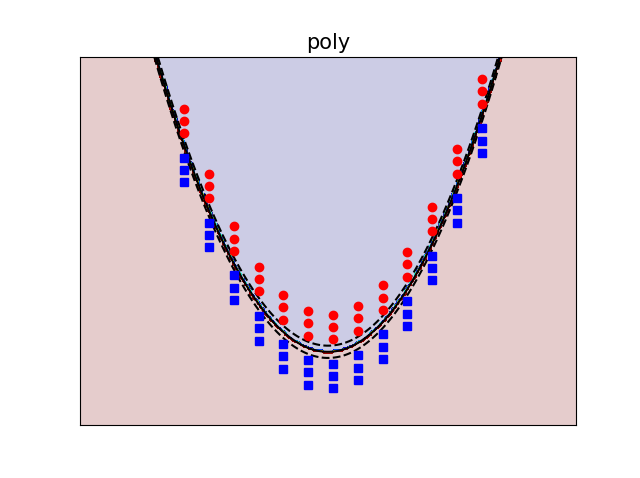
• Sigmoid:

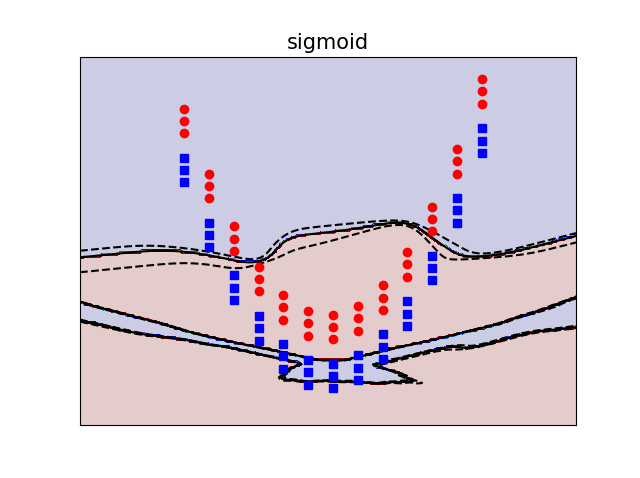
Ngoài các kernel phổ biến trên, còn rất nhiều kernel khác như String kernel, Chi-square kernel, histogram intersection kernel,…

Độ tốt của các Kernel là việc rất khó nói(Có rất nhiều bài báo nghiên cứu việc này), tuy nhiên RBF(Gaussian kernel) thường được dùng nhiều nhất.
Andrew Ng có một vài “tricks” như sau:

• Use linear kernel (or logistic regression) when number of features is larger than number of observations(number of training examples).
• Use gaussian kernel when number of observations is larger than number of features.
• If number of observations is larger than 50,000 speed could be an issue when using gaussian kernel; hence, one might want to use linear kernel.

Kinh nghiệm cá nhân của mình là thử hết :)))
Neural network có thể làm được (đến tốt) mọi trường hợp trên nhưng có lẽ sẽ chậm hơn.
Thêm 1 chú ý nữa, neural network dùng convex optimization.

Kernel rbf có thể hơi khó hiểu. Mọi người có thể tham khảo thêm tại đây.

Tài liệu tham khảo

1. Stanford CS229 Lecture Notes (Notes 3)
2. Convex Optimization – Boyd and Vandenberghe, Cambridge University Press, 2004.
3. The Elements of Statistical Learning: Data Mining, Inference, and Prediction
4. Machine Learning Cơ bản