Bài viết này mang tính khái niệm nhiều hơn là học thuật (như các bài trước). Tôi hy vọng người đọc sẽ có một cái nhìn khái quát và dễ hiểu nhất.

Perceptron

Bí thuật của trí tuệ nhân tạo hiện đại, nền tảng của nền tảng!

Perceptron là một trong những thuật toán sơ khai nhất để thực hiện phép phân loại 2 lớp, ý tưởng ban đầu là vẽ ra một đường phân loại (đường thẳng trên mặt phẳng, mặt phẳng trong không gian hay siêu phẳng (hyperplane) trong không gian đa chiều).

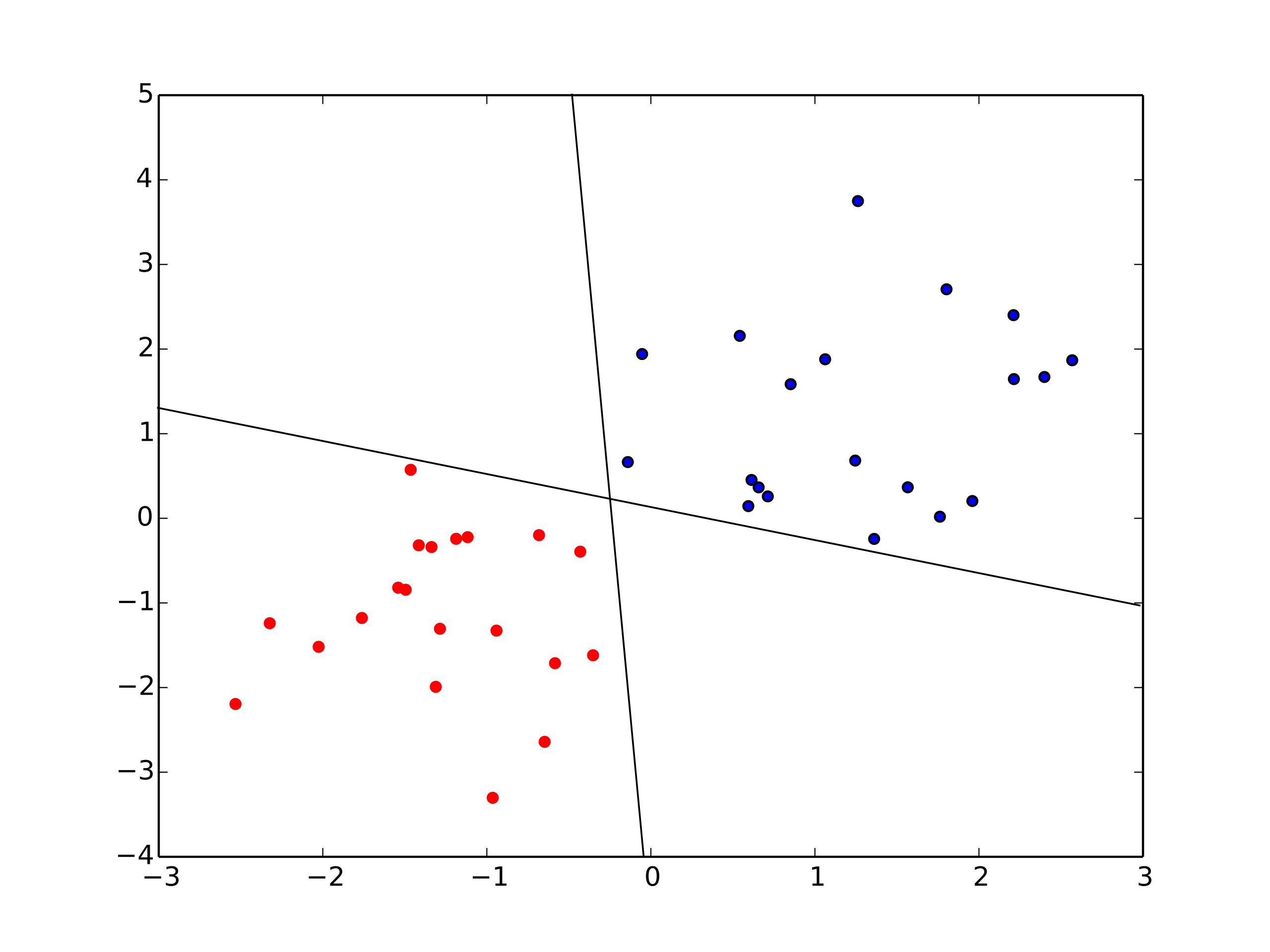
Trong hình minh hoạ trên, ta thấy phân loại 2 lớp của các điểm đỏ và xanh rất rõ ràng, có thể có nhiều đường thẳng giúp phân loại 2 lớp này, bài toán đơn giản này tưởng chừng quá dễ để giải và không phù hợp với thực tế vì nhiều bài toán, các điểm phân loại không tách biệt mà xen lẫn vào nhau. Tuy nhiên, nó là nền tảng chính để phát triển các thuật toán mạng neural sau nay, tương tự với máy tính hiện đại chỉ hoạt động bằng các phép toán luận lý cơ bản trên 2 bit giá trị 1 và 0 rõ ràng nhưng có thể giải quyết các bài toán phức tạp.

Thuật toán Peceptron (PLA)

Thuật toán Perceptron Learning Algorithm (PLA) có ý tưởng đơn giản là tìm một đường thẳng để phân chia mặt phẳng 2 chiều thành 2 phần, phân loại các điểm dữ liệu vào 2 phần này. Đối với không gian nhiều chiều hơn, thuật toán sẽ tìm 1 siêu phẳng (hyperplane) để phân loại trong không gian.

Công thức của một đường thẳng trong mặt phẳng \(Oxy\) sẽ là

\[ax + by + c = 0\]

Tuy nhiên, để phân biệt giữa nhãn và tham số nhiều chiều, ta sẽ gọi 2 trục x và y trong mặt phẳng là \(x_1\) và \(x_2\). 2 tham số lúc này sẽ được viết thành \(w_1\) và \(w_2\), công thức của 1 đường thẳng trong không gian 2 chiều mới \(Ox_1x_2\) được viết lại là:

\[f(x) = w_1x_1 + w_1x_2 + c = 0\]

Ta được biết rằng, đường thẳng \(f(x)\) này phân cách mặt phẳng thành 2 nữa mặt phẳng, các điểm dữ liệu ở cùng nữa mặt phẳng khi thay vào giá trị của đường thẳng sẽ cùng dấu (âm hoặc dương). Thuật toán PLA sẽ tìm cách tìm các giá trị của tham số \(w\) và \(b\) sao cho tất các các điểm trên cùng lớp sẽ có cùng dấu.

Để đơn giản hơn, người ta gán cho 2 lớp với giá trị âm và dương, nếu điểm nào trong lớp có giá trị khác với giá trị mặc định của lớp đó thì cần sửa lại đường thẳng. Mã giả của thuật toán như sau:

1. Khởi tạo 1 đường thẳng bất kỳ bằng cách gán giá trị w và b ngẫu nhiên

2. Lặp các điểm cho đến khi tìm được kết quả:
    2.1 Kiểm tra xem các điểm trong lớp có bị phân loại sai không
    2.2 Nếu có, cập nhật w và b theo công thức: 
        w = w + y * x
        b = b + y
3. Khi không còn điểm nào sai, xuất ra kết quả w và b

Tại sao lại là w = w + y * x và b = b + y?

Hiểu đơn giản, đây là cách “sai ở đâu, sửa ở đó”.

Giải thích: việc chỉ update các điểm dữ liệu phân loại sai, nghĩa là y và và giá trị của \(y\) sẽ trái dấu với \(w*x+b\), việc cộng tham số với giá trị trái dấu của nó sẽ làm nó nhỏ dần và tiến về 0 hoặc ngược dấu với giá trị hiện tại. Khi đó, tất cả các điểm dữ liệu sai sẽ được lặp lại và sửa cho đến khi đúng.

Thuật toán với Python

import numpy as np

def perceptron(X, y, lr=0.1, epochs=1000):
    """
    Thuật toán Perceptron Learning Algorithm (PLA)

    Args:
        X: Ma trận dữ liệu đầu vào (mỗi hàng là một điểm dữ liệu)
        y: Vector nhãn lớp (-1 hoặc 1)
        lr: Learning rate (tốc độ học)
        epochs: Số lượng epochs (vòng lặp huấn luyện)

    Returns:
        w: Vector trọng số đã học được
        b: Bias đã học được
    """
    m, n = X.shape  # Lấy số lượng điểm dữ liệu và số lượng đặc trưng
    w = np.zeros(n)  # Khởi tạo vector trọng số
    b = 0  # Khởi tạo bias

    for _ in range(epochs):
        for i in range(m):
            x = X[i]
            y_pred = np.sign(np.dot(w, x) + b)  # Tính toán dự đoán

            if y_pred != y[i]:  # Nếu dự đoán sai
                w += lr * y[i] * x  # Cập nhật trọng số
                b += lr * y[i]  # Cập nhật bias

    return w, b

# Ví dụ sử dụng:
X = np.array([
    [0, 0],
    [0, 1],
    [1, 0],
    [1, 1]
])
y = np.array([-1, -1, 1, 1])
w, b = perceptron(X, y)

print("Trọng số đã học được:", w)
print("Bias đã học được:", b)

Ở thuật toán python này, tôi có thêm biến learning rate lr để giúp việc update tham số từ từ chậm hơn, tránh việc số nhảy loạn khi x lớn, khó hội tụ.

Neural Network

Multilayer perceptron

Từ đường thẳng đến đường cong

Perceptron đã giải quyết được bài toán phân loại tuyến tính (đường thẳng) rồi, nhưng chúng ta mong muốn có một mô hình mạnh mẽ hơn, có thể giải quyết được các bài toán phân loại mà các đường phân loại (hay hyperplane trong không gian đa chiều) là những đường cong phức tạp không theo phương trình nhất định hoăc là các điểm dữ liệu có thể không tách biệt hoàn toàn. Cách nào để giải quyết được nó đây?

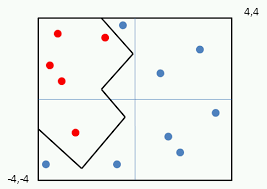
Ý tưởng đơn giản cho việc ước lượng 1 đường cho để tách biệt 2 phần dữ liệu là vẽ nhiều đoạn thẳng, đoạn cong và các tia, các đoạn càng nhiều thì đường cong phân tách sẽ càng mượt. Vậy cách nào để biến đường thẳng tuyến tính thành các đoạn thẳng hay đoạn cong? câu trả lời là dùng thêm các hàm phi tuyến tính làm hàm kích hoạt (activation function) ở đầu ra của các perceptron, tiêu biểu như hàm Relu, có công thức là \[y = x ( \text{ nếu } x > 0) \\ y = 0 (\text{ nếu } x <= 0)\]

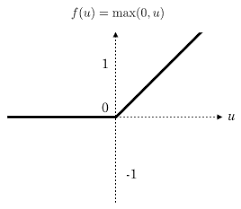
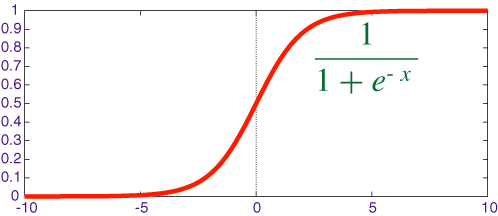
Ngoài Relu thì ta có thể sử dụng nhiều hàm phi tuyến khác như Sin, Sigmoid (có đề cập ở bài Logistic Regression, Tanh,…) để giúp bẻ cong hoặc giới hạn sự tuyến tính của output của 1 perceptron, kết hợp nhiều perceptron có hàm kích hoạt sẽ giúp mô hình có thể có ước lượng bất kỳ đường cong nào.

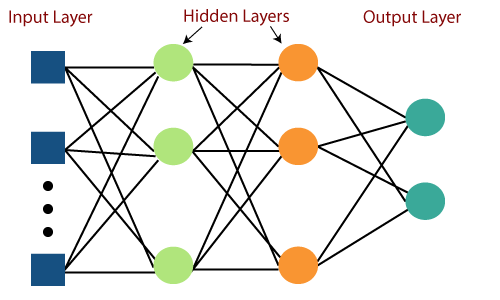
Ngoài việc tăng số lượng perceptron, ta có thể tăng nhiều lớp perceptron với output của lớp trước là input của lớp sau, các mô hình sẽ học được nhiều thông tin và mối quan hệ phức tạp hơn giữa các input và các perceptron.

Một mạng lưới các perceptron liên kết với nhau được gọi là mạng nơ-ron hay neural network.

Loss function

“Thước Đo” Sai Số của Neural network

Trong thuật toán PLA, các tham số được điều chỉnh để đường phân loại (hoặc hyperplane trong không gian đa chiều) sang hướng của điểm dữ liệu bị phân loại sai, ta cũng không biết nó sai nhiều hay ít (ở xa hay gần). Đồng thời, với các tập dữ liệu có sự trùng lặp (overlap) giữa các class như hình minh hoạ dưới, rất khó để tìm ra 1 đường phân loại chính xác 2 lớp.

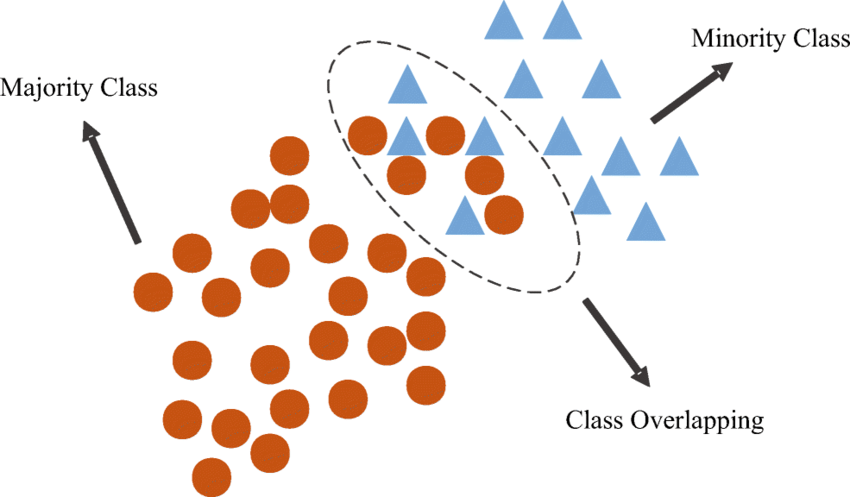
Hàm mất mát (loss function) cho phép mô hình biết được các điểm dữ liệu nào là sai ít hoặc sai nhiều, các điểm sai nào là chấp nhận được để nhanh chóng tìm ra đường phân loại tối ưu.

Các loại Loss Function phổ biến:

Tùy thuộc vào loại bài toán (phân loại hay hồi quy) và đặc thù của dữ liệu, chúng ta có thể lựa chọn các loại Loss Function khác nhau. Dưới đây là một số hàm mất mát phổ biến:

Mean Squared Error (MSE): Thường được sử dụng trong các bài toán hồi quy, MSE tính toán trung bình bình phương của sai số giữa giá trị dự đoán và giá trị thực tế.

\[\sum_{i=1}^{D}(x_i-y_i)^2\]

Mean Absolute Error (MAE): Tương tự như MSE, nhưng MAE tính trung bình giá trị tuyệt đối của sai số. MAE ít bị ảnh hưởng bởi các điểm dữ liệu ngoại lai (outliers) hơn so với MSE.

\[\sum_{i=1}^{D}(x_i-y_i)\]

Cross-Entropy Loss: Thường được sử dụng trong các bài toán phân loại, Cross-Entropy Loss đo lường mức độ khác biệt giữa phân phối xác suất dự đoán của mô hình và phân phối xác suất thực tế của các lớp.

\[-\sum_{c=1}^My_{o,c}\log(p_{o,c})\]

Hinge Loss: Được sử dụng trong các mô hình Support Vector Machine (SVM), Hinge Loss khuyến khích mô hình tìm ra một lề (margin) lớn nhất có thể giữa các lớp.

Việc lựa chọn Loss Function phù hợp là một yếu tố quan trọng ảnh hưởng đến hiệu suất của mô hình. Không có một Loss Function nào là tốt nhất cho mọi bài toán, việc lựa chọn phụ thuộc vào đặc thù của dữ liệu và mục tiêu của bài toán.

Backpropagation

Bí quyết “Luyện tập” của Neural network

Backpropagation là một thuật toán tối ưu hóa dựa trên gradient (gradient-based optimization) được sử dụng để điều chỉnh các trọng số \(w\) và bias \(b\) của MLP trong quá trình huấn luyện. Nó hoạt động bằng cách tính toán gradient của hàm mất mát (loss function) theo từng trọng số và bias, sau đó cập nhật các tham số này theo hướng ngược với gradient để giảm thiểu sai số giữa dự đoán của mô hình và giá trị thực tế.

Quá trình Backpropagation:

Feedforward (Lan truyền xuôi): Đầu tiên, dữ liệu đầu vào được đưa vào lớp đầu vào của MLP và lan truyền qua các lớp ẩn đến lớp đầu ra, tạo ra một dự đoán.

Tính toán sai số (Error Calculation): Sai số giữa dự đoán của mô hình và giá trị thực tế được tính toán bằng hàm mất mát. Hàm mất mát thường được sử dụng là Mean Squared Error (MSE) cho bài toán hồi quy hoặc Cross-Entropy Loss cho bài toán phân loại.

Backpropagation (Lan truyền ngược): Gradient của hàm mất mát theo từng trọng số và bias được tính toán bằng cách sử dụng quy tắc chuỗi (chain rule) của đạo hàm. Gradient này cho biết hướng và độ lớn cần thiết để cập nhật các tham số nhằm giảm thiểu sai số.

Cập nhật trọng số (Weight Update): Trọng số và bias được cập nhật theo hướng ngược với gradient, với một hệ số tỷ lệ được gọi là learning rate (tốc độ học). Learning rate quyết định mức độ “nhanh” mà mô hình điều chỉnh các tham số.

Mã giả của thuật toán như sau:

1. Khởi tạo mạng nơ-ron với các trọng số (weights) và bias ngẫu nhiên.
2. Lặp lại cho mỗi epoch:
   a. Lặp lại cho mỗi mẫu dữ liệu trong tập huấn luyện:
      i. Lan truyền xuôi (feedforward):
         - Tính toán đầu ra của từng lớp dựa trên đầu vào và các trọng số, bias.
         - Lưu lại các giá trị trung gian (đầu vào và đầu ra của từng nơ-ron).
      ii. Tính toán sai số (error) tại lớp đầu ra:
         - So sánh đầu ra dự đoán với nhãn thực tế để tính toán sai số.
      iii. Lan truyền ngược (backpropagation):
         - Từ lớp đầu ra trở về lớp đầu vào, tính toán gradient của hàm mất mát (loss function) theo từng trọng số và bias.
         - Sử dụng quy tắc chuỗi (chain rule) để tính toán gradient.
      iv. Cập nhật trọng số và bias:
         - Cập nhật trọng số và bias dựa trên gradient và learning rate (tốc độ học).

import numpy as np

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

def sigmoid_derivative(x):
    return x * (1 - x)

def backpropagation(X, y, weights, biases, learning_rate):
    """
    Thuật toán Backpropagation cho một mạng nơ-ron đơn giản (1 lớp ẩn).

    Args:
        X: Ma trận dữ liệu đầu vào (mỗi hàng là một mẫu dữ liệu).
        y: Vector nhãn thực tế.
        weights: Danh sách các ma trận trọng số của từng lớp.
        biases: Danh sách các vector bias của từng lớp.
        learning_rate: Tốc độ học.
    """

    # Lan truyền xuôi
    hidden_layer_input = np.dot(X, weights[0]) + biases[0]
    hidden_layer_output = sigmoid(hidden_layer_input)
    output_layer_input = np.dot(hidden_layer_output, weights[1]) + biases[1]
    output = sigmoid(output_layer_input)

    # Tính toán sai số tại lớp đầu ra
    error = y - output

    # Lan truyền ngược
    output_layer_delta = error * sigmoid_derivative(output)
    hidden_layer_delta = output_layer_delta.dot(weights[1].T) * sigmoid_derivative(hidden_layer_output)

    # Cập nhật trọng số và bias
    weights[1] += hidden_layer_output.T.dot(output_layer_delta) * learning_rate
    biases[1] += np.sum(output_layer_delta, axis=0, keepdims=True) * learning_rate
    weights[0] += X.T.dot(hidden_layer_delta) * learning_rate
    biases[0] += np.sum(hidden_layer_delta, axis=0, keepdims=True) * learning_rate

Thuật toán backpropagation có cách hoạt động tương tự như Gradient Descent method ở bài Logistic Regression.

Deep Neural Network

We need to go deeper!

Nếu Multilayer Perceptron (MLP) là một tòa nhà hai tầng, thì Deep Neural Network (DNN) chính là một tòa nhà chọc trời với nhiều tầng ẩn (hidden layers). Chính sự sâu sắc này đã tạo nên sức mạnh vượt trội của DNN trong việc học hỏi và xử lý thông tin phức tạp.

Deep Neural Network (DNN) là gì?

DNN là một loại mạng nơ-ron nhân tạo với nhiều lớp ẩn (thường là từ 3 lớp trở lên). Mỗi lớp ẩn đóng vai trò như một bộ lọc, trích xuất các đặc trưng trừu tượng hơn từ dữ liệu đầu vào. Càng nhiều lớp ẩn, DNN càng có khả năng học được các biểu diễn phức tạp và tinh tế hơn của dữ liệu.

Huấn luyện Deep Neural Network

Để giải quyết các bài toán phức tạp hơn với nhiều chiều dữ liệu hơn, các mối quan hệ phức tạp giữa các đặt trưng dữ liệu và các đầu ra phức tạp hơn, ta cần một mô hình phức tạp với nhiều lớp hơn, đòi hỏi lượng tài liệu (dữ liệu để học) lớn hơn và khả năng tính toán lớn hơn nhiều lần.

May mắn thay, sau khi internet ra đời, lượng thông tin con người có được trên nhiều lĩnh vực cũng đa dạng và nhiều hơn, đồng thời công nghệ tính toán cũng phát triển hơn nhiều với các bộ xử lý đồ hoạ (GPU) cho phép xử lý nhanh và nhiều phép tính hơn CPU nhiều lần.

Ngoài việc phát triển về dữ liệu và tính toán, các nghiên cứu gần đây cũng tập trung về các kiến trúc mạng neuron khác nhau cho các bài toán và loại dữ liệu khác nhau. Các kỹ thuật huấn luyện và các thư viện tính toán với máy tính.

Một số kiến trúc mạng nổi tiếng gồm:

• Convolutional Neural Network - CNN: thường dùng chính cho các tác vụ về ảnh và video.
• Recurrent Neural Network - RNN: thường dùng cho các tác vụ có tính tuần tự như timeseries, câu văn bản
• Autoencoder: dùng để huấn luyện các mô hình về giải mã hoặc nhúng, ứng dụng nhiều lĩnh vực.
• Generative Adversarial Network - GAN: Dùng cho các tác vụ tạo sinh như sinh ảnh, sinh văn bản, vân vân.
• Transformers: Chuyên cho các tác vụ về văn bản với hiệu quả tốt hơn các mạng RNN.

Một số kỹ thuật huấn luyện mô hình:

• regularization, dropout: cho phép giảm overfit
• Data augmentation: cho phép đa dạng hoá dữ liệu đầu vào
• Batch Normalization: giúp chuẩn hoá output của đầu ra ở các lớp ẩn, giúp mô hình huấn luyện nhanh hơn và tránh bị Internal Covariate Shift,
• Thuật toán optimization: SGD, Adam, Momentum
• Transfer Learning: Chuyển kiến thức từ một mô hình có sẵn sang một mô hình khác.
• Ensemble Learning: Kết hợp nhiều mô hình lại với nhau.

Trong các blog tiếp theo, chúng ta sẽ cùng đi sâu về các mô hình Deep learning hiện đại và tìm hiểu về các mô hình ngôn ngữ lớn Large Language Models - LLM

Tài liệu tham khảo

Perceptron:

Rosenblatt, F. (1958). The perceptron: A probabilistic model for information storage and organization in the brain. Psychological Review, 65(6), 386-408. Minsky, M., & Papert, S. (1969). Perceptrons: An introduction to computational geometry. MIT Press. Multilayer Perceptron (MLP):

Rumelhart, D. E., Hinton, G. E., & Williams, R. J. (1986). Learning representations by back-propagating errors. Nature, 323(6088), 533-536. Cybenko, G. (1989). Approximation by superpositions of a sigmoidal function. Mathematics of Control, Signals, and Systems, 2(4), 303-314. Neural Networks:

Haykin, S. S. (2009). Neural networks and learning machines (3rd ed.). Pearson Education. Goodfellow, I., Bengio, Y., & Courville, A. (2016). Deep learning. MIT Press. Backpropagation:

Werbos, P. J. (1974). Beyond regression: New tools for prediction and analysis in the behavioral sciences (Doctoral dissertation, Harvard University). Rumelhart, D. E., Hinton, G. E., & Williams, R. J. (1986). Learning representations by back-propagating errors. Nature, 323(6088), 533-536.